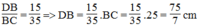Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: \(\frac{DB}{DC}=\frac{AB}{AC}\)(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
uy ra: \(\frac{DB}{DB+DC}=\frac{15}{15+20}\)(tính chất tỉ lệ thức)
Suy ra: \(\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}cm\)
\(\Rightarrow DC=BC-BD=25-\frac{75}{7}=\frac{100}{7}cm\)
b. Kẻ AH ⊥ BC
Ta có: SABD = 1/2 AH.BD; SADC = 1/2 AH.DC
Suy ra :\(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}\)
Mà\(\frac{DB}{DC}=\frac{15}{20}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ADC}}=\frac{3}{4}\)
Hình tự vẽ lấy nhé
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
\(\Rightarrow\frac{DB}{DC}=\frac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
\(\Rightarrow\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}\left(cm\right)\)
b) Kẻ \(AH\perp BC\)
Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)
\(S_{ACD}=\frac{1}{2}AH.CD\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.CD}=\frac{BD}{DC}\)
Mà \(\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}\left(đpcm\right)\)
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
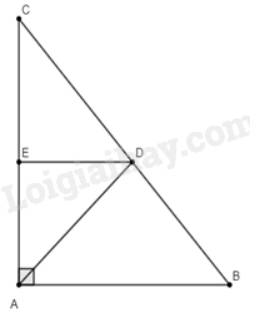
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2
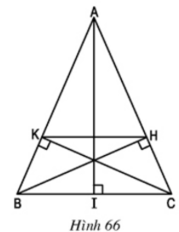
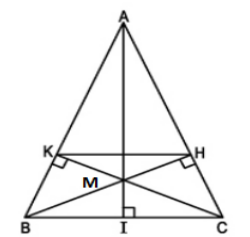
A B C K H I
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)
a) Xét tam giác ABC có:
BD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)
\(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)
b) Kẻ đường cao AH của tam giác ABC
\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)
a: Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)
mà BD+CD=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)
Bài 1:Cho tam giác ABC vuông tại A có AB = 3cm ; BC = 5cm . AD là đg phân giác của tam giác ABC . có:
A. BD = 20/7 cm; CD = 15/7cm.
B. BD = 15/7 cm; CD = 20/7 cm
C. BD = 1,5 cm; CD = 2,5 cm
D. BD = 2,5 cm; CD = 1,5 cm
Bài 2: Cho tâm giác ABC có BD là đg phân giác , AB = 8cm , BC = 10cm , CA = 6cm . Ta có:
A. DA = 8/3 ; DC = 10/3
B. DA = 10/3; DC = 8/3
C. DA = 4; DC = 2
D. DA = 2,5; DC = 2,5
Bài 3: Cho tâm giác ABC có góc A là 120, AD là đg phân giác. Chứng minh đc rằng:
A. 1/AB + 1/AC = 2/AD
B. 1/AD + 1/AC = 1/AB
C. 1/ AB + 1/AC = 1/AD
D. 1/AB + 1/AC = 1
Bài 4: Cho tâm giác ABC . Tia phân giác trong của góc A cắt BC tại D . Cho AB = 6, AC = x , BD = 9, BC = 21. Hãy chọn kết quả đúng về độ dài x :
A. x = 14
B. x = 12
C. x = 8
D. Một kết quả khác
Bài 5: Tâm giác ABC có cạnh AB = 15 cm , AC = 20cm, BC = 25cm. Đg phân giác của góc BAC cắt cạnh BC tại D. Vậy độ dài DB là :
A.10
B.10_5/7
C.14
D.14_2/7
Bài 6: Tam giác ABC có cạnh AB bằng 15cm, AC = 20cm, BC = 25cm. Đg phân giác góc BAC cắt BC tại D. Vậy tỉ số diện tích của 2 tâm giác ABD và ACD là:
A. 1/4
B. 1/2
C. 3/4
D.1/3
Bài 7: Độ dài các cạnh tâm giác BAC tỉ lệ với 2:3:4 BD là tâm giác trong ứng với cạnh ngắn nhất AC, chia AC thành 2 đoạn AD và CD . nếu độ dài là 10, thế thì độ dài của đoạn thẳng dài hơn trong 2 đoạn AD và CD là:
A. 3,5
B.5
C. 40/7
D.6
Bài 8:
Cho tam giác ABC có góc B = 50 , M là trung điểm của BC . Tia phân giác của góc AMB cắt AB tại E . Tia phân giác của góc AMC cắt AC tại F. Phát biêủ nào sau đây là đúng:
A. ME//AC
B. góc AEF = 50°
C. Góc FMC = 50°
D. MB/MA= FA/FC
Bài 9: Cho tam giác ABC vuông tại A có AB= 8cm , BC = 10cm , CD là đg phân giác. Ta chứng tỏ đc:
A. DA = 3cm
B. DB = 5cm
C. AC = 6cm
D. Cả 3 đều đúng
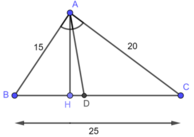
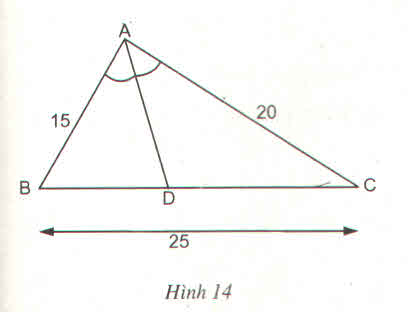
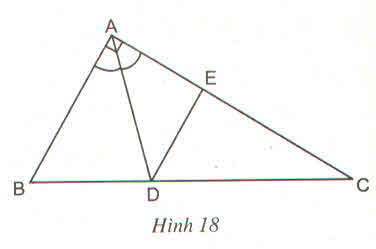
Trong △ ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: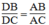
(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên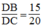
Suy ra: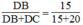
(tính chất tỉ lệ thức)
Suy ra: