Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vật ở VTCB lò xo giãn ra một đoạn: \(\Delta l\)
\(\Rightarrow\Delta l=\frac{g}{\omega^2}\Leftrightarrow\omega\sqrt{\frac{g}{\Delta l}}\)
Tần số của con lắc lò xo:
\(\Rightarrow f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}\)

Đáp án A
Phương pháp: Sử dụng công thức tính chu kì dao động của con lắc lò xo treo thẳng đứng
T = 2 π ∆ l g

\(f=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}=\frac{1}{2\pi}\sqrt{\frac{\pi^2}{0.16}}=1.25Hz\)

\(\Delta l=5cm\)
Vị trí có lực đẩy đàn hồi lần thứ nhất chính là vị trí lò xo bắt đầu bị nén. Tức là qua vị trí -\(x=-\Delta l\).
M -10 10 N -5 ^
Vị trí ban đầu t = 0 tại M ứng với góc (-90 độ).
Vị trí lực đầy đàn hồi lần thứ nhất tại N x = -5 cm.
=> \(\varphi=\pi+\frac{\pi}{6}=\frac{7\pi}{6}\Rightarrow t=\frac{\varphi}{\omega}=\frac{7\pi}{6.10\pi}=\frac{7}{60}s.\)
sai rồi bạn ơi, lực đẩy max là lúc vật ở vị trí -A nhé, denta phi sẽ là 3π/2, và t sẽ là 3/20s
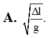
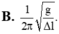
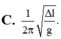
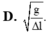
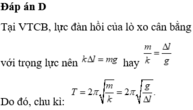
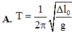
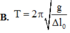
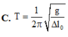
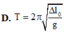

Chọn đáp án D.
Ta có: f = 1 2 π g Δ l 0 .