Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

+ \(\omega=\sqrt{\dfrac{g}{l}}=\sqrt{\dfrac{9,8}{0,2}}=7(rad/s)\)
t = 0 vật qua li độ 30 theo chiều dương \(\Rightarrow \varphi = -\dfrac{\pi}{6}\) rad
Vậy PT li độ góc: \(\alpha=6\cos(7t-\dfrac{\pi}{3})(^0)\)
+ Áp dụng: \(v=\sqrt{2gl(\cos\alpha-\cos\alpha_0)}\)
\(\Rightarrow v=\sqrt{2.9,8.0,2(\cos3^0-\cos6^0)}=...\)

\(W_t=\frac{mgl\alpha^2}{2}=\frac{4.1,2.0,05^2}{2}=6.10^{-3}J\)

Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)

Đáp án A
+ Lực căng dây của con lắc T = mg 3 cosα − 2 cosα 0 → α = α 0 T = mgcosα 0

 =2 7,1 cm/s
=2 7,1 cm/s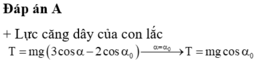
Đáp án D
+ Biểu thức tính lực căng dây của con lắc đơn T = mg(3cosα – 2cos α o ).