Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:
- A B λ < k < A B λ ⇔ - 10 1 , 5 < k < 10 1 , 5 ⇔ - 6 , 67 < k < 6 , 67 ⇒ k = 0 ; ± 1 , ± 2 , . . . . , ± 6
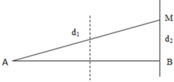
+ Ta có: S A M B = 1 2 A B . M B ⇒ ( S A M B ) m i n ⇔ ( M B ) m i n ⇔ M thuộc cực đại ứng với kmax => d1 – d2 = 6λ = 9cm.
+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
A B 2 + d 2 2 = d 1 2 ⇔ 10 2 + d 2 2 = ( d 2 + 9 ) 2 ⇒ d 2 = 19 18 c m = M B ⇒ S A M B = 1 2 A B . M B = 1 2 . 10 . 19 18 = 5 , 28 c m 2

Đáp án D
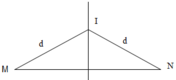
Giả sử phương trình sóng tại M và N là: u M = A 1 cos ω t u N = A 1 cos ( ω t + π ) = - A 2 cos ω t
Phương trình sóng truyền từ M đến I và từ N đến I: u M I = A 1 cos ( ω t - 2 π d λ ) u N I = - A 2 cos ( ω t - 2 π d λ )
Phương trình sóng tổng hợp tại I:
u I = u M I + u N I = A cos ω t = A 1 cos ( ω t - 2 π d λ ) - A 2 cos ( ω t - 2 π d λ ) = ( A 1 - A 2 ) cos ω t - 2 π d λ ⇒ A = A 1 - A 2

Biên độ sóng tại một điểm M bất kì cách nguồn O1, O2 lần lượt các đoạn d1, d2 là
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}+\frac{\triangle\varphi}{2\pi})|\)
\(\triangle\varphi = 0\)
Biên độ tại điểm có cực đại giao thoa \(A_{Mmax} = A_0=> 2a =2cm.\)
Để biên độ sóng tại M
\(A_M = 1,2 cm=> |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = 1,2\)
=> \(\cos \pi(\frac{d_2-d_1}{\lambda})= 0,6.\)
\(=> \pi.(\frac{d_2-d_1}{\lambda}) = \frac{53}{180}.\pi+k2\pi\)
=> \(d_2-d_1 = (2k + 0,29)\lambda\ \ (1).\)
M nằm trên đoạn thẳng \(O_1O_2\) tức là (không được tính hai nguồn)
\(-O_1O_2 < d_2-d_1 < O_1O_2\)
Thay (1) vào ta được
\(-O_1O_2 < (2k+0,29)\lambda < O_1O_2\)
=> \(-1,745 < k < 1,455\)
=> \(k = -1,0,1.\)

\(\lambda = v/f = 2cm.\)
Số điểm dao động cực đại thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (k+\frac{\triangle\varphi)}{2 \pi}\lambda < AB \\ \Rightarrow -10 < k\lambda < 10. \\ \Rightarrow -5 < k < 5.\\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3,4.\)
Có 9 điểm dao động với biên độ cực đại.
Số điểm dao động cực tiểu thỏa mãn:
\(-AB < d_2-d_1 < AB \Rightarrow -AB < (2k+1+\frac{\triangle\varphi}{\pi})\frac{\lambda}{2} < AB \\ \Rightarrow -10 < (2k+1)\lambda/2 < 10 \\ \Rightarrow -5,5 < k < 4,5 \\ \Rightarrow k = -5,-4,-3,-2,-1,0,1,2,3,4.\)
Có 10 điểm dao động với biên độ cực tiểu.

Chọn đáp án C
@ Lời giải:
+ Nếu hai nguồn sóng cùng pha thì những điểm cực tiểu giao thoa nằm tại vị trí: d 2 − d 1 = k + 0,5 λ với k nguyên

M A B
Giữa M và đường trung trực của AB có hai đường cực đại khác tức là M nằm ở đường cực đại thứ k = 3. (Vì đường trung trực của AB với AB cùng pha là cực đại với k = 0)
=> \(AM - BM = 3 \lambda\)
=> \(20 - 15.5 = 3 \lambda \)
=>\(3 \frac{v}{f} = 4,5cm\)
=>\(f = \frac{3v}{4,5} = 20Hz.\)
Chọn đáp án. A

Như ta biết, bản chất của giao thoa sóng là tổng hợp dao động do 2 nguồn truyền đến.
Do đó, dao động tại M là tổng hợp 2 dao động do A và B truyền đến.
Bước sóng: \(\lambda = 30/10 = 3cm\)
Độ lệch pha 2 dao động từ A, B truyền đến là: \(\Delta \varphi = 2\pi\frac{d_2-d_1}{\lambda}=2\pi\frac{13,5-10,5}{3}=2\pi\) (rad)
Biên độ tổng hợp: \(A_M=\sqrt{A_A^2+A_B^2+2A_AA_B\cos\Delta\varphi}=\sqrt{2^2+2^2+2.2.2.\cos2\pi}=4\)(cm)
Đáp án B
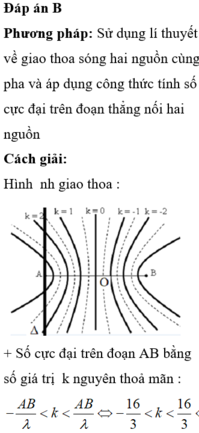


Chọn B
+ Với hiện tượng giao thoa hai nguồn kết hợp cùng pha thì trung điểm của đoạn thẳng nối hai nguồn là một cực đại.