Bài 1 :
1, Tính giá trị biểu thức :
a, A =\(\frac{\left(1+2+3+...+2019\right)\cdot\left(12\cdot3,4-6,8\cdot6\right)}{\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2019}}\)
b, B =\(\frac{4}{3\cdot5}-\frac{6}{5\cdot7}+\frac{8}{7\cdot9}-\frac{10}{9\cdot11}+\frac{12}{11\cdot13}-...+\frac{100}{99\cdot101}\)
2, Cho : A = \(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2018}\)
B = \(\frac{1}{2017}+\frac{2}{2016}+\frac{3}{2018}+...+\frac{2016}{2}+\frac{2017}{1}\)
CMR : A : B là số nguyên
Bài 2 :
a, Tìm x biết : 2019 - | x-2019 | = x
b, Tìm \(x\inℤ\)để \(ℚ\)=\(\frac{4x-3}{3x+1}\)có giá trị là số tự nhiên
c, Tìm các số nguyên tố x,y sao cho : 15x + 10y = 2000
Bài 3 :
a, Cho ba số a,b,c thỏa mãn : \(\frac{ab}{a+b}=\frac{bc}{b+c}=\frac{ca}{c+a}\)
Tính M : \(\frac{\left(ab+bc+ca\right)^{1008}}{a^{2019}+b^{2019}+c^{2019}}\)
b, Cho x,y,z ; a,b,c thỏa mãn : \(\frac{x}{a+2b+c}=\frac{y}{2a+b-c}=\frac{ℤ}{4a-4b+c}\)
CMR : \(\frac{a}{x+2y+Z}=\frac{b}{2x+y-Z}=\frac{Z}{4x-4y+Z}\)
Bài 4 : Cho hàm số : y = f(x) thỏa mãn : f (x1+x2) = f (x1) +f (x2)và f (x) - x.f (-x) = x+1 \(\left(\forall x\inℝ\right)\)
a, CMR : M ( 0 ; 1 ) thuộc đồ thị hàm số
b, Tính f (2019)
Bài 5 : cho đoạn thẳng AB ; D là trung điểm của AB . Trên cùng 1 nửa mặp phẳng bờ chứa AB vẽ 2 tia Ax , By cùng \(\perp\)AB. Trên Ax ,By lần lượt lấy C,D sao cho \(\widehat{COD}\)= 90o . Tia CD cắt tia DB tại E :
1, CMR : a,\(\Delta CDE\)cân
b, CO là tia phân giác của \(\widehat{ACD}\)
2, Vẽ \(OM\perp CD\). CMR : AMB vuông tại M
3, Gọi S là diện tích \(\Delta AMB\). Giả sử AB = a . Tìm giá trị lớn nhất của S (theo a)
( ai trả lời nhanh nhất mk tick cho )



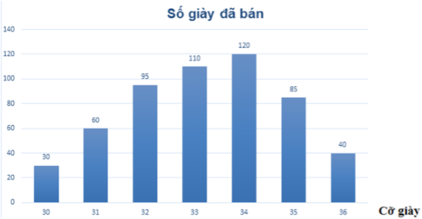
Cửa hàng đó bán được tất cả số đôi giày là:
30 + 60 + 95 + 110+ 120 + 85 + 40 = 540 (đôi giày)
Đáp án cần chọn là: C