Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 17. Một vật nhỏ dao động điều hòa theo một quỹ đạo thẳng dài 14 cm với chu kì 1 s. Từ thời điểm vật qua vị trí có li độ 3,5 cm theo chiều dương đến khi gia tốc của vật đạt giá trị cực tiểu lần thứ hai, vật có tốc độ trung bình là
A. 27,0 cm/s.
B. 26,7 cm/s.
C. 28,0 cm/s.
D. 27,3 cm/s.
\(A=\dfrac{14}{2}=7\left(cm\right);T=1s\Rightarrow\omega=2\pi\left(rad/s\right)\)
Gia tốc vật đạt giá trị cực tiểu <=> vật qua VTCB, nghĩa là từ thời điểm vật qua vị trí có li độ 3,5cm theo chiều dương đến khi vật qua VTCB lần thứ 2.
Ta có: \(x=3,5\Rightarrow\dfrac{x}{A}=\dfrac{3,5}{7}=\dfrac{1}{2}\Rightarrow arc\cos\left(\dfrac{1}{2}\right)=\varphi_1=\dfrac{\pi}{3}\left(rad\right)\)
\(\Rightarrow\varphi=\varphi_1+\dfrac{3\pi}{2}=\dfrac{\pi}{3}+\dfrac{3\pi}{2}=\dfrac{11}{6}\pi\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{11\pi}{6.2\pi}=\dfrac{11}{12}\left(s\right)\)
\(S=3,5+3A=3,5+7.3=24,5\left(cm\right)\)
\(\Rightarrow v_{tb}=\dfrac{S}{t}=\dfrac{24,5}{\dfrac{11}{12}}=26,72\Rightarrow B\)

Biên độ A = 14 : 2 = 7cm.
Gia tốc của vật đạt giá trị cực tiểu là a = \(-\omega^2A\)(khi ở biên độ dương)(bạn cần phân biệt giá trị cực tiểu với độ lớn cực tiểu).
Biểu diễn bằng véc tơ quay ta có:
O x M N 60 0 7 -7 3,5
Chất điểm qua li độ 3,5 cm theo chiều dương ứng với véc tơ quay qua N, có gia tốc cực tiểu khi véc tơ quay qua M.
Quãng đường đi được là: S \(v_{TB}= \frac{S}{t}=\frac{31,5}{\frac{7}{6}}=27\)= 3,5 + 4.7 = 31,5 cm (do qua M 2 lần)
Thời gian: t = \(\frac{60}{360}T + T = (\frac{1}{6}+1).1 = \frac{7}{6}\)s.
Tốc độ trung bình \(v_{TB} = \frac{S}{t}=\frac{31,5}{\frac{6}{7}}=27\)(cm/s)

Vật dao động theo quỹ đạo thẳng dài 14 cm tức là \(2A = 14cm => A = 7cm.\)
Dựng đường tròn tương ứng với dao động của vật (Chiều dương ngược chiều kim đồng hồ)
7 -7 3,5 φ N M x 0 P
Điểm \(M\) và \(N\) đều có li độ là 3,5 cm nhưng chỉ có điểm \(M\) chuyển động theo chiều dương của trục x.
\(a_{min} = - \omega ^2 x_{min}\)=> vị trí vật có gia tốc cực tiểu là \(x_{min} = - 7 cm \) tương ứng với điểm \(P\) trên hình vẽ.
Vật sẽ đi từ \(M \rightarrow P \rightarrow P.\)
\(M \rightarrow P: t_1 = \frac{\varphi}{\omega} = \frac{\pi + \pi/3}{2\pi} = \frac{2}{3}s; S_1 = 3,5+ 2.7 = 17,5cm.\)
\(P \rightarrow P: t_2 = T= 1s; S_2 = 4.A= 4.7 = 28cm.\)
Vận tốc trung bình là \(v = \frac{quãng đường đi được}{thơi gian}\)
=> \(v = \frac{S_1+S_2}{t_1 + t_2} = \frac{17.5+28}{2/3+1} = 27,3cm/s.\)
Chọn đáp án.A.27,3cm.
câu này đáp án là 27 cm nhé
và vị trí gia tốc có giá trị cực tiểu là biên dương chứ không phải biên âm
![]()

Đáp án D
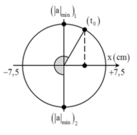
+ Biên độ dao động của vật A=0,5L =0,5.14=7cm.
+ Gia tốc của vật có độ lớn cực tiểu khi vật đi qua vị trí cân bằng.
=> Biểu diễn các vị trí tương ứng trên đường tròn.
+ Từ hình vẽ, ta có:
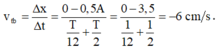

Tốc độ trung bình của vật là \(v = \frac{\text{quãng đường đi được}}{t}\)
(chú ý là tốc độ trung bình khác với vận tốc trung bình vì vận tốc trung bình = \(\frac{x_{cuoi}-x_{dau}}{t}\))
Dùng đường tròn để tìm quãng đường và thời gian đi
4 -4 2 3 2 3 - M N a π/6 π/6 H K
Vật đi được từ điểm N (\(x = -2\sqrt{3}\) hường theo chiều dương của trục x) đến điểm M (\(x = 2\sqrt{3}\) hướng theo chiều dương của trục x) tức là ứng với cung \(\stackrel\frown{NaM}\)
Quãng đường đi được là: \(S = HK= 2\sqrt{3}+ 2\sqrt{3} = 4\sqrt{3}cm.\)
Thời gian đi \(t = \frac{\varphi}{\omega} = \frac{\pi/3+\pi/3}{8\pi} = \frac{1}{12}s.\)
Vận tốc trung bình là \(v = \frac{4\sqrt{3}}{1/12} = 48 \sqrt{3}cm/s.\)
Chọn đáp án. D
Làm sao biết được là pi/6 vậy ạ. C chỉ giúp mình được không ạ?

Biên độ: A = 16/4 = 4cm.
Biểu diễn dao động điều hòa bằng véc tơ quay. Khi vật đi từ x1 đến x2 thì véc tơ quay một góc là:
\(30+60=90^0\)
Thời gian tương ứng: \(\frac{90}{360}T=\frac{1}{4}.0,4=0,1s\)
Tốc độ trung bình: \(v_{TB}=\frac{S}{t}=\frac{2+2\sqrt{3}}{0,1}=54,64\)(cm/s)

với A = 14 2 = 7cm