
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) =
=
.
b) =
=
.
c) =
=
.
d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)

a) Giả sử ∆x là số gia của số đối tại x0= 1. Ta có:
∆y = f(1 + ∆x) - f(1) = 7 + (1 + ∆x) - (1 + ∆x)2 - (7 + 1 - 12) = -(∆x)2 - ∆x ;
= - ∆x - 1 ;
=
(- ∆x - 1) = -1.
Vậy f'(1) = -1.
b) Giả sử ∆x là số gia của số đối tại x0= 2. Ta có:
∆y = f(2 + ∆x) - f(2) = (2 + ∆x)3 - 2(2 + ∆x) + 1 - (23 - 2.2 + 1) = (∆x)3 + 6(∆x)2 + 10∆x;
= (∆x)2 + 6∆x + 10;
=
[(∆x)2 + 6∆x + 10] = 10.
Vậy f'(2) = 10.
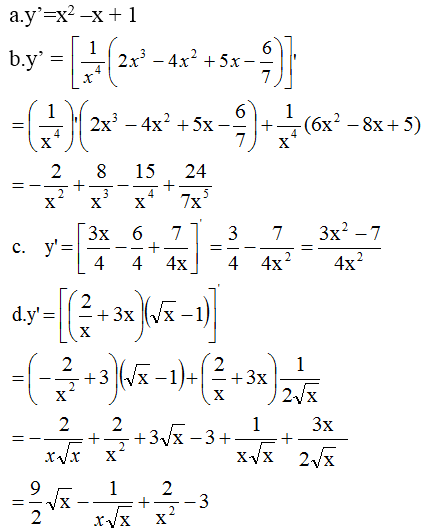
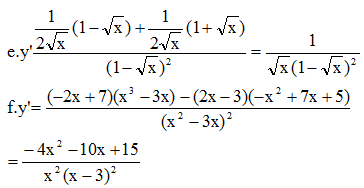
Cách 1 : y = 3x5 (8 - 3x2)
= 3x5.8 – 3x5.3x2 = 24x5 – 9x7
⇒ y’ = (24x5 – 9x7)’
= (24x5)' – (9x7)’
= 24.5x4 – 9.7x6
= 120x4 – 63x6.
Cách 2 : Áp dụng công thức tính đạo hàm của tích :
⇒ y’ = [(3x5)’].(8 – 3x2) + 3x5.[(8 – 3x2)’]
= 3.5x4(8 – 3x2) + 3x5.[(8)’ – (3x2)’]
= 15x4(8 – 3x2) + 3x5.(0 – 3.2x)
= 15x4.8 – 15x4.3x2 + 3x5.(-6x)
= 120x4 – 45x6 – 18x6
= 120x4 – 63x6.