Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Gọi d1, d2 là khoảng cách từ M đến 2 nguồn ( M thuộc đường tròn và thỏa yêu cầu)
+ M thuộc đường tròn nên góc AMB là góc vuông → d12 + d22 = ( 8 2 ) 2
+ M dao động với biên độ cực đại nên: d1 - d2 = kl
Mà λ = v . T = 0 , 6 . 2 π 30 π = 0 , 04 m m
+ Giải hệ phương trình trên ta được: 2d22 + 8kd2 + 16k2 - 128 = 0
Chỉ có k = 0 là thỏa mãn → d1 = d2 = 8 cm
+ M dao động cùng pha với nguồn nên d1 + d2 = 2k’l → k’ = 2
Vậy có tất cả 2 điểm.
Đáp án D

+ Gọi d1, d2 là khoảng cách từ M đến 2 nguồn (M thuộc đường tròn và thỏa yêu cầu)
+ M thuộc đường tròn nên góc AMB là góc vuông ® d12 + d22 = 8 2 2
+ M dao động với biên độ cực đại nên: d1- d2 = kl
Mà λ = v . T = 0 , 6 . 2 π 30 π = 0 , 04 m
+ Giải hệ phương trình trên ta được: 2d22 + 8kd2 + 16k2- 128 = 0
Chỉ có k = 0 là thỏa mãn ® d1 = d2 = 8 cm
+ M dao động cùng pha với nguồn nên d1 + d2 = 2k’l® k’ = 2
Vậy có tất cả 2 điểm.
Chọn đáp án D

Chọn A

trên đoạn AB có 5 “bó sóng” vớ O là bụng của bó trung tâm. Các bó đối xứng nhau qua một bụng thì cùng pha nên có hai điểm khác cùng pha với O

Đáp án C
+ Bước sóng của sóng λ = 2 π v ω = 5 c m
+ Số dãy cực đại giao thoa
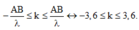
Có 7 dãy cực đại ứng với ![]()
+ Điều kiện để M cực đại và cùng pha với hai nguồn:
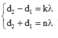

A B C D
$\lambda = \dfrac{3}{2}$
Vị trí cực đại thoả mãn: $(20-20\sqrt {2} \le (k+0,5)\lambda \le 20 \Rightarrow $ số $k=19$
Vậy có 19 điểm dao động biên độ cực đại trên đoạn AD.

Chọn C
+ Bước sóng của sóng λ = v 2 π ω = 3 , 5 c m
Số cực tiểu giao thoa trên đoạn thẳng nối hai nguồn ngược pha:
- A B λ ≤ k ≤ A B λ ⇔ - 5 , 7 ≤ k ≤ 5 , 7
Vậy có 11 điểm

- Bước sóng của sóng:
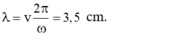
- Số cực tiểu giao thoa trên đoạn thẳng nối hai nguồn ngược pha:
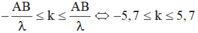
- Vậy có 11 điểm

Chọn đáp án A
f = ω 2 π = 25 H z ⇒ λ = v f = 75 25 = 3 c m
Hai nguồn dao động ngược pha → điều kiện để điểm M dao động cực đại là ∆ d = ( 2 k + 1 ) λ 2
→ -12 ≤ (2k + 1).1,5 ≤ 12 → -4,5 ≤ k ≤ 3,5 → k = -4,...0,...3 → trong khoảng AB có 8 điểm dao động với biên độ cực đại.
Mỗi đường cực đại cắt đường tròn đường kính AB tại hai điểm nên số điểm dao động có biên độ cực đại trên đường tròn đường kính AB là 16
- Gọi d1, d2 là khoảng cách từ M đến 2 nguồn (M thuộc đường tròn và thỏa yêu cầu)
+ M thuộc đường tròn nên góc AMB là góc vuông
+ M dao động với biên độ cực đại nên: d1 - d2 = kλ
- Giải hệ phương trình trên ta được:
+ Chỉ có k = 0 là thỏa mãn ⇒ d1 = d2 = 8 cm
+ M dao động cùng pha với nguồn nên:
- Vậy có tất cả 2 điểm.