Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thước kẹp bằng thép : Sai số tuyệt đối của 150 độ chia tương ứng với 150 mm trên thước kẹp khi nhiệt độ của thước tăng từ t 0 = 0 ° C đến t 1 = 50 ° C là :
∆ l = l 0 α t h t 1 ≈ 150.11. 10 - 6 .50 = 82,5 μ m

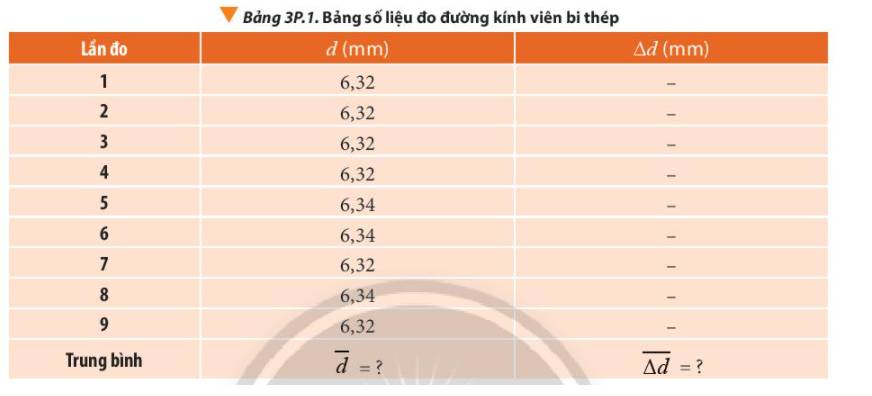
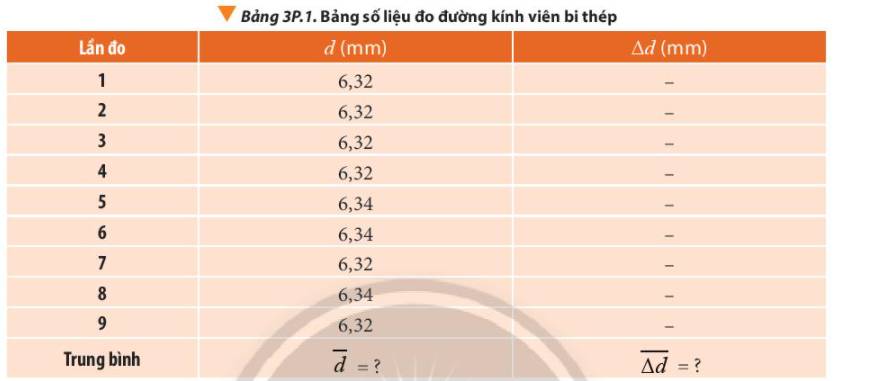
Giá trị trung bình của đường kính viên bi thép là:
\(\overline d = \frac{{{d_1} + {d_2} + ... + {d_9}}}{9} \approx 6,33(mm)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {d_1} = \left| {\overline d - {d_1}} \right| = \left| {6,33 - 6,32} \right| = 0,01(mm) = \Delta {d_2} = \Delta {d_3} = \Delta {d_4} = \Delta {d_7} = \Delta {d_9}\\\Delta {d_5} = \left| {\overline d - {d_5}} \right| = \left| {6,33 - 6,34} \right| = 0,01(mm) = \Delta {d_6} = \Delta {d_8}\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta d} = \frac{{\Delta {d_1} + \Delta {d_2} + ... + \Delta {d_9}}}{9} = 0,01(mm)\)
Sai số tuyệt đối của phép đo là:
\(\Delta d = \overline {\Delta d} + \Delta {d_{dc}} = 0,01 + 0,02 = 0,03(mm)\)

B3: to = 20C
\(\Delta l=l_o\alpha\left(50-20\right)=0,0033m\)
=> phải để hở 1 khe lớn hơn hoặc = 0,0033m
B1: a, \(\Delta l=l_o\alpha\left(40-20\right)=0,00033m\)
b, \(l=\Delta l+l_o=1,50033m\)
B5: Ta co: \(V=V_o\left[1+3\alpha\left(t-t_o\right)\right]\)
=> \(\frac{m}{D}=\frac{m}{D_o}\left[1+3\alpha\left(500-0\right)\right]\)
=> D \(\approx6885,4\)
B2: \(l-l_o=l_o\alpha\left(t-0\right)\)
=> \(l_o\alpha\left(t-0\right)=0,0008\)
=> \(t\approx72,7^oC\)

Ta có:
+ Ở 350C chiều dài của thước là: l 2 = l 0 1 + α t 2
Nếu ở 50C thì chiều dài thước là: l 1 = l 0 1 + α t 1
+ Sai số do ảnh hưởng của nhiệt độ là do thước dãn nở một đoạn: ∆ l = l 2 - l 1 = α l 0 ∆ t → ∆ l = l 2 1 + α t 2 α ∆ t = 88 , 45 1 + 2 , 3 . 10 - 5 . 35 + 273 . 2 , 3 . 10 - 5 . 35 - 5 = 0 , 0606 c m
Chiều dài đúng của vật là: l ' = l 2 - ∆ l = 88 , 45 - 0 , 0606 = 88 , 3894 c m
Phần trăm sai số của phép đo: δ = ∆ l l ' . 100 % = 0 , 0606 88 , 3894 . 100 % ≈ 0 , 07 %
Đáp án: B

Thước kẹp bằng hợp kim Inva : Hợp kim Inva có hệ số nở dài α i n v = 0,9. 10 - 6 K - 1 Áp dụng công thức tính tương tự phần (a), ta xác định được sai số tuyệt đối của thước kẹp này khi nhiệt độ của thước tăng từ t 0 = 0 ° C đến t 1 = 50 ° C là :
∆ l’ = l 0 α i n v t 1 ≈ 150.0,9. 10 - 6 .50 = 6,75 μ m