Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 2 kích thước của hình chữ nhật là x và y(ĐK:x,y>0)
Diện tích của hình chữ nhật là xy
Nếu tăng chiều rộng thêm 3m và chiều dài giảm đi 4 m thì diện tích của hình chữ nhật là (x+3).(y-4).
Theo bài ra ta có hệ phương trình:
xy=240
{ ⇔x=12;y=20 Vậy chiều rộng HCN là 12,chiều dài HCN là 20
(x+3).(y-4)=xy
Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.Gọi chiều dài là x (m), chiều rộng là y (m) (Đk: 240>y>x>0).
Ta có: xy=240 và
(x+3)(y-4)=240
Giải hệ phương trình trên ( rút thế), ta được chiều dài là 20 m, chiều rộng 12m.
Trình bày thì bạn theo cách giáo viên hướng dẫn nhé.

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng
240
m
2
⇒
Δ
=
3
2
–
4
.
1
.
(
-
180
)
=
729
⇒ Chiều dài mảnh đất là: 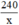 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
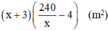
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
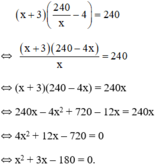
Có a = 1; b = 3; c = -180
Phương trình có hai nghiệm:
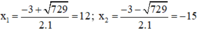
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Gọi chiều dài của mảnh đất hình chữ nhật là x (m, x > 4)
Khi đó chiều rộng của mảnh đất hình chữ nhật là \(\frac{240}{x}\left(m\right)\)
Khi tăng chiều rộng 3m, giảm chiều dài 4m thì diện tích mảnh đất là:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)\)
Do diện tích không đổi nên ta có phương trình:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)=240\)
\(\Rightarrow240+3x-\frac{960}{x}-12=240\)
\(\Rightarrow3x^2-12x-960=0\Rightarrow\orbr{\begin{cases}x=20\left(n\right)\\x=-16\left(l\right)\end{cases}}\)
Vậy chiều dài mảnh đất là 20m, chiều rộng mảnh đất là 12m.

Bài giải:
Gọi chiều rộng của mảnh đất là x (m), x > 0.
Vì diện tích của mảnh đất bằng 240 m2 nên chiều dài là: (m)
Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì mảnh đất mới có chiều rộng là x + 3 (m), chiều dài là (240/X - 4) (m) và diện tích là:
(x + 3)( 240/x- 4) ( m2 )
Theo đầu bài ta có phương trình: (x + 3)(240/x - 4) = 240
Giải phương trình:
Từ phương trình này suy ra:
-4x2 – 12x + 240x + 720 = 240x hay:
x2 + 3x – 180 = 0
Giải phương trình: ∆ = 32 + 720 = 729, √∆ = 27
x1 = 12, x2 = -15
Vì x > 0 nên x2 = -15 không thỏa mãn điều kiện của ẩn. Do đó chiều rộng là 12m, chiều dài là: 240 : 12 = 20(m)
Trả lời: Mảnh đất có chiều rộng là 12m, chiều dài là 20m.
Bài giải:
Gọi chiều rộng của mảnh đất là x (m), x > 0.
Vì diện tích của mảnh đất bằng 240 m2 nên chiều dài là: (m)
Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì mảnh đất mới có chiều rộng là x + 3 (m), chiều dài là ( - 4) (m) và diện tích là:
(x + 3)( - 4) ( m2 )
Theo đầu bài ta có phương trình: (x + 3)( - 4) = 240
Giải phương trình:
Từ phương trình này suy ra:
-4x2 – 12x + 240x + 720 = 240x hay:
x2 + 3x – 180 = 0
Giải phương trình: ∆ = 32 + 720 = 729, √∆ = 27
x1 = 12, x2 = -15
Vì x > 0 nên x2 = -15 không thỏa mãn điều kiện của ẩn. Do đó chiều rộng là 12m, chiều dài là: 240 : 12 = 20 (m)
Trả lời: Mảnh đất có chiều rộng là 12m, chiều dài là 20m.

Gọi chiều rộng của mảnh đất là x (m) ĐK : x > 0
Vì diện tích của mảnh đất là 240m2 nên chiều dài là 240/x (m)
Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì
Do diện tích không đổi
nên ta có phương trình
(x + 3) (240/x - 4) = 240
giải phương trình trên ta có x1 = 12(TMĐK )
x2 = -15 ( loại )
vây chiều rộng mảnh đất là 12m ,chiều dài là 20m
Gọi chiều rộng của mảnh đất là x (m) ĐK : x > 0
Vì diện tích của mảnh đất là 240m2 nên chiều dài là 240/x (m)
Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì
Do diện tích không đổi
nên ta có phương trình
(x + 3) (240/x - 4) = 240
giải phương trình trên ta có x1 = 12(TMĐK )
x2 = -15 ( loại )
vây chiều rộng mảnh đất là 12m ,chiều dài là 20m

Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là a, b ( m ) ( \(0< a,b< 110\) )
Theo bài, ta có hệ phương trình: \(\hept{\begin{cases}a-b=17\\ab=110\end{cases}}\)
Đặt \(c=-b\)\(\Rightarrow\hept{\begin{cases}a+c=17\\a.c=-110\end{cases}}\)
\(\Rightarrow\)a và c là nghiệm của của phương trình: \(x^2-17x-110=0\)
\(\Delta=\left(-17\right)^2-4.1.\left(-110\right)=729\)
\(\Rightarrow\sqrt{\Delta}=\sqrt{729}=27\)
\(\Rightarrow x_1=\frac{-\left(-17\right)+27}{2}=\frac{17+27}{2}=\frac{44}{2}=22\)
\(x_2=\frac{-\left(-17\right)-27}{2}=\frac{17-27}{2}=\frac{-10}{2}=-5\)
\(\Rightarrow a=x_1=22\); \(c=x_2=-5\)
mà \(-b=c\)\(\Rightarrow b=-c=-\left(-5\right)=5\)
Vậy chiều dài là 22m, chiều rộng là 5m
Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng 240 m2 ⇒ Chiều dài mảnh đất là: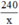 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
Có a = 1; b = 3; c = -180 ⇒ Δ = 32 – 4.1.(-180) = 729
Phương trình có hai nghiệm:
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).