Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tứ giác nhận được theo nhát cắt AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

Tứ giác nhận được theo nhát cắt AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

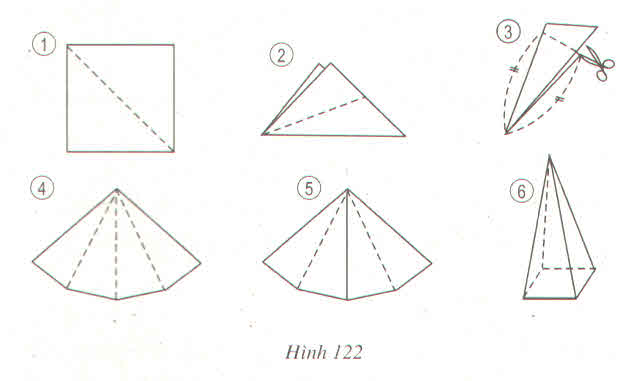
Vì gấp làm 1 phần tư và cắt 1 nhát kéo thành 1 tam giác nên khi mở ra sẽ là 4 tam giác bằng nhau
=> tứ giác đó có 4 cạnh là 4 cạnh huyền của 4 tam giác bằng nhau nên tứ giác đó có 4 cạnh bằng nhau
=> tứ giác đó là hình thoi

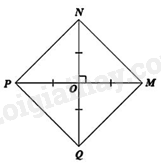
Vì \(OM = ON = OP = OQ\) nên \(O\) là trung điểm của \(NQ\) và \(MP\) và \(MP = NQ\)
Xét tứ giác \(MNPQ\) có hai đường chéo \(NQ\) và \(MP\) cắt nhau tại trung điểm \(O\) (cmt)
Suy ra \(MNPQ\) là hình bình hành
Mà \(MP = NQ\) (cmt) nên \(MNPQ\) là hình chữ nhật
Lại có \(MP \bot NQ\) (gt) nên \(MNPQ\) là hình vuông

- Trong trường hợp a:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
- Trong trường hợp b:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.

Xét \(\Delta\)ABC có: D là trung điểm của AB
M là trung điểm của BC
\(\Rightarrow\)DM là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DM\)//AC hay DM//AE
Ta có : M là trung điểm của BC
E là trung điểm của CA
\(\Rightarrow\)ME là đường trung bình của \(\Delta\)ABC
\(\Rightarrow\)ME//AB hay ME//AD
Xét tứ giác ADME có: DM//AE(cmt)
ME//AD(cmt)
\(\Rightarrow\)ADME là hình bình hành
Nếu \(\Delta\)ABC cân tại A có đường trung tuyến AM
\(\Rightarrow\)AM đồng thời là tia phân giác của \(\widehat{A}\)
Xét hình bình hành ADME có đường chéo AM là tia phân giác của \(\widehat{A}\)(cmt)
\(\Rightarrow\)ADME là hình thoi
Nếu \(\Delta\)ABC vuông tại A
\(\Rightarrow\widehat{A}=90^0\)
Xét hình bình hành ADME có \(\widehat{A}=90^0\)(cmt)
\(\Rightarrow\)ADME là hình chữ nhật
d/ Xét \(\Delta ABC\) vuông tại A, đường trung tuyến AM
\(\Rightarrow AM=\frac{1}{2}BC\)(Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng 1/2 cạnh huyền)
Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A ta có:
BC2=AB2+AC2
\(\Leftrightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Leftrightarrow BC=\sqrt{6^2+8^2}\)
\(\Leftrightarrow BC=10\left(cm\right)\)
Khi đó:AM=\(\frac{1}{2}.BC=\frac{1}{2}.10=5\left(cm\right)\)
Vậy trong trường hợp tam giác ABC vuông tại A, AB=6cm và AC=8cm thì AM=5cm

c: Ta có: \(EF\le KE+KF\)
\(\Leftrightarrow EF\le\dfrac{DC+AB}{2}\)
Dấu '='xảy ra khi E,K,F thẳng hàng
hay EF//AB//DC
Suy ra: ABCD là hình thang
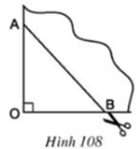
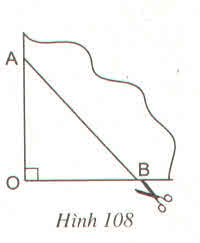
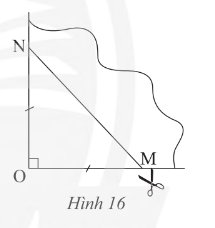
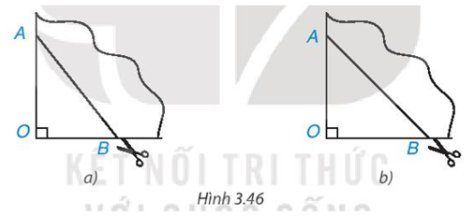
- Tứ giác nhận được theo nhát cắt của AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.
- Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.