K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
QD
31 tháng 3 2017
Bài 7. a) sin 3x - cos 5x = 0 ⇔ cos 5x = sin 3x ⇔ cos 5x = cos (
- 3x) ⇔
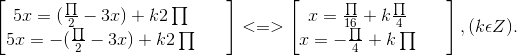
b) tan 3x . tan x = 1 ⇔ 
. Điều kiện : cos 3x . cos x # 0.
Với điều kiện này phương trình tương đương với
cos 3x . cos x = sin 3x . sinx ⇔ cos 3x . cos x - sin 3x . sinx = 0 ⇔ cos 4x = 0.
Do đó
tan 3x . tan x = 1 ⇔ 
⇔ cos 2x = 
⇔ cos 4x = 0
⇔ 
TN
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 10 2019
\(\Leftrightarrow\sqrt{3}cos5x-\left(sin5x+sinx\right)-sinx=0\)
\(\Leftrightarrow\sqrt{3}cos5x-sin5x=2sinx\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}cos5x-\frac{1}{2}sin5x=sinx\)
\(\Leftrightarrow sin\left(\frac{\pi}{3}-5x\right)=sinx\)
\(\Leftrightarrow...\)
N
11 tháng 9 2016
a)pt\(\Leftrightarrow cosx\left(cosx+1\right)+sinx.sin^2x=0\)
\(\Leftrightarrow cosx\left(cosx+1\right)+sinx\left(1-cos^2x\right)=0\)
\(\Leftrightarrow\left(cosx+1\right)\left(cosx+sinx-sinx.cosx\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}cosx=1\Leftrightarrow x=\pi+k2\pi\\cosx+sinx-sinx.cosx=0\left(\cdot\right)\end{array}\right.\)
Xét pt(*):
Đặt \(t=cosx+sinx,t\in\left[-\sqrt{2};\sqrt{2}\right]\Rightarrow sinx.cosx=\frac{t^2-1}{2}\)
(*) trở thành:\(t^2-2t-1=0\Leftrightarrow\left[\begin{array}{nghiempt}t=1-\sqrt{2}\\t=1+\sqrt{2}\left(L\right)\end{array}\right.\)
+)\(t=1-\sqrt{2}\Rightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1-\sqrt{2}\\ \Leftrightarrow\left[\begin{array}{nghiempt}x=-\frac{\pi}{4}+arcsin\left(\frac{-2+\sqrt{2}}{2}\right)+k2\pi\\x=-\frac{5\pi}{4}-arcsin\left(\frac{-2+\sqrt{2}}{2}\right)+k2\pi\end{cases}\left(k\in Z\right)}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2020
c/
\(\Leftrightarrow sin3x=-cosx\)
\(\Leftrightarrow sin3x=sin\left(x-\frac{\pi}{2}\right)\)
\(\Rightarrow\left[{}\begin{matrix}3x=x-\frac{\pi}{2}+k2\pi\\3x=\frac{3\pi}{2}-x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=\frac{3\pi}{8}+\frac{k\pi}{2}\end{matrix}\right.\)
d/
\(\Leftrightarrow2sinx.cosx+\sqrt{3}sinx=0\)
\(\Leftrightarrow sinx\left(2cosx+\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=-\frac{\sqrt{3}}{2}=cos\left(\frac{5\pi}{6}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{5\pi}{6}+k2\pi\\x=-\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2020
a/
\(\Leftrightarrow\left[{}\begin{matrix}cos2x+1=0\\cos2x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=-2\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow2x=\pi+k2\pi\)
\(\Rightarrow x=\frac{\pi}{2}+k\pi\)
b/
\(\Leftrightarrow cos5x=sin40^0\)
\(\Leftrightarrow cos5x=cos50^0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=50^0+k360^0\\5x=-50^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=10^0+k72^0\\x=-10^0+k72^0\end{matrix}\right.\)
A
4 tháng 10 2018
cos5x+2sinxcosx+2sin3xsin2x=0
⇔cos5x+2sinxcosx+\(\dfrac{1}{2}\)(cosx-cos5x)*2=0
⇔cos5x+2sinxcosx+cosx-cos5x=0
⇔cosx(1+2sinx)=0
⇔cosx=0 hoặc sinx=\(\dfrac{-1}{2}\)
⇔x=\(\dfrac{\Pi}{2}+k\Pi\) hoặc x=\(\dfrac{-1}{6}\Pi+k2\Pi\) hoặc x=\(\dfrac{7}{6}\Pi+k2\Pi\) với k∈Z
AH
Akai Haruma
Giáo viên
4 tháng 10 2018
Lời giải:
\(\cos 5x+2\sin x\cos x+2\sin 3x\sin 2x=0\)
\(\Leftrightarrow \cos (3x+2x)+2\sin x\cos x+2\sin 3x\sin 2x=0\)
\(\Leftrightarrow \cos 3x\cos 2x-\sin 3x\sin 2x+2\sin x\cos x+2\sin3x\sin 2x=0\)
\(\Leftrightarrow (\cos 3x\cos 2x+\sin 3x\sin 2x)+2\sin x\cos x=0\)
\(\Leftrightarrow \cos (3x-2x)+2\sin x\cos x=0\)
\(\Leftrightarrow \cos x(1+2\sin x)=0\)
\(\Rightarrow \left[\begin{matrix} \cos x=0\\ 1+2\sin x=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} \cos x=0\\ \sin x=\frac{-1}{2}\end{matrix}\right.\)
\(\Rightarrow \left[\begin{matrix} x=k\pi+\frac{\pi}{2}\\ x=\frac{-\pi}{6}+2k\pi\\ x=\frac{7\pi}{6}+2k\pi\end{matrix}\right.\) (k nguyên)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2020
1.
\(\Leftrightarrow cos3x=-\frac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=40^0+k120^0\\x=-40^0+k120^0\end{matrix}\right.\)
\(\Rightarrow x=\left\{40^0;160^0;80^0\right\}\)
2.
Bạn coi lại đề, số \(-\sqrt{3}\) bên vế trái ko hề hợp lý, toán cho cấp 1 như vầy còn được chứ cấp 3 chắc ko ai cho đề kiểu vậy đâu
3.
\(\Leftrightarrow\sqrt{3}sin3x-cos3x=-sin5x-\sqrt{3}cos5x\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin3x-\frac{1}{2}cos3x=-\left(\frac{1}{2}sin5x+\frac{\sqrt{3}}{2}cos5x\right)\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{6}\right)=sin\left(-5x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\frac{\pi}{6}=-5x-\frac{\pi}{3}+k2\pi\\3x-\frac{\pi}{6}=\frac{4\pi}{3}+5x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{48}+\frac{k\pi}{4}\\x=-\frac{7\pi}{12}+k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2020
c/
\(\Leftrightarrow\sqrt{2}sin\left(3x-\frac{\pi}{4}\right)=\frac{\sqrt{3}}{\sqrt{2}}\)
\(\Leftrightarrow sin\left(3x-\frac{\pi}{4}\right)=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}3x-\frac{\pi}{4}=\frac{\pi}{3}+k2\pi\\3x-\frac{\pi}{4}=\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{7\pi}{36}+\frac{k2\pi}{3}\\x=\frac{11\pi}{36}+\frac{k2\pi}{3}\end{matrix}\right.\)
d/
\(\Leftrightarrow2sinx.cosx+1-2sin^2x=1\)
\(\Leftrightarrow2sinx\left(cosx-sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{4}+k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2020
a/
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin5x-\frac{1}{2}cos5x=-1\)
\(\Leftrightarrow sin\left(5x-\frac{\pi}{6}\right)=-1\)
\(\Leftrightarrow5x-\frac{\pi}{6}=-\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\frac{\pi}{15}+\frac{k2\pi}{5}\)
b/
\(\Leftrightarrow\frac{1}{2}sinx-\frac{\sqrt{3}}{2}cosx=\frac{1}{2}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\x-\frac{\pi}{3}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
sin3x - cos5x = 0
Vậy phương trình có hai họ nghiệm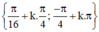
(k ∈ Z).