Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

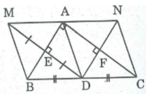
Tứ giác AEDF là hình chữ nhật
⇒ DE // AC; DF // AB
Trong ∆ ABC, ta có: DB = DC (gt)
Mà DE // AC
Suy ra: AE = EB (tính chất đường trung bình của tam giác)
Lại có: DF // AB và DB = DC
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM, ta có: AE = EB (chứng minh trên)
ED = EM (vì AB là trung trực DM)
Suy ra tứ giác ADBM là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mặt khác: AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi (vì có hai đường chéo vuông góc)
Xét tứ giác ADCN, ta có: AF = FC (chứng minh trên)
DF = FN (vì AC là đường trung trực DN)
Suy ra tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Lại có: AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

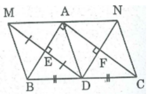
Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = 1/2 AB; AF = 1/2 AC
Nên AE = AF ⇒ AB = AC
Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.

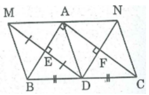
Điểm M và điểm D đối xứng qua trục AB
Suy ra AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM ⇒ ∠ (AED) = 90 0
Điểm D và điểm N đối xứng qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN ⇒ AC ⊥ DN ⇒ ∠ (AFD) = 90 0
Mà ∠ (EAF) = 90 0 (gt). Vậy tứ giác AEDF là hình chữ nhật (vì có 3 góc vuông).

a)
DEA = EAF = AFD = 900
=> AEDF là hình chữ nhật
b)
D là trung điểm của BC
mà DE // AC (DE _I_ AB; AC _I_ AB)
=> E là trung điểm của AB
mà E là trung điểm của MD (M đối xứng D qua AB)
=> ADBM là hình bình hành
mà AB _I_ MD (M đối xứng D qua AB)
=> ADBM là hình thoi
c)
D là trung điểm của BC
mà DF // AB (DF _I_ AC; AB _I_ AC)
=> F là trung điểm của AC
mà F là trung điểm của ND (N đối xứng D qua AC)
=> ADCN là hình bình hành
mà AC _I_ ND (N đối xứng D qua AC)
=> ADCN là hình thoi
=> AN // BC
mà AM // BC (ADBM là hình thoi)
=> M, A, N thẳng hàng
AN = CD (ADCN là hình thoi)
AM = BD (ADBM là hình thoi)
=> CD = BD (D là trung điểm của BC)
=> AM = AN
=> M đối xứng N qua A
d)
AEDF là hình vuông
<=> AD là tia phân giác của BAC
mà AD là đường trung tuyến của tam giác ABC vuông tại A (D là trung điểm của BC)
=> Tam giác ABC vuông cân tại A

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a: D đối xứng với M qua AB
nên DM vuông góc với AB tại trung điểm của DM
=>E là trung điểm của DM và AB là phân giác của góc DAM(2)
=>AD=AM; BD=BM
mà DA=DB
nên AD=AM=BD=BM
D đối xứng với N qua AC
nên AC vuông góc với DN tại trung điểm của DN
=>AC là phân giác của góc NAD(1) và F là trung điểm của DN
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nên AEDF là hình chữ nhật
b: Từ (1), (2) suy ra góc MAN=2*90=180 độ
=>M,A,N thẳng hàng
mà AM=AN
nên A là trung điểm của MN
c: Để AEDF là hình vuông thì AD là phân giác của góc FAE
mà AD là trung tuyến ứng với BC
nên ΔABC cân tại A
=>AB=AC
Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng qua điểm A.