Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

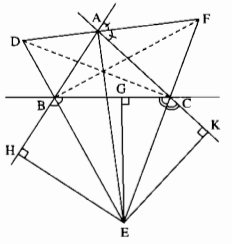
a) E thuộc tia phân giác của ˆCBHCBH^
⇒⇒ EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ˆBCKBCK^
⇒⇒ EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
⇒⇒ E thuộc tia phân giác của ˆBACBAC^ mà E # A
Vậy AE là tia phân giác của ˆBACBAC^
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
⇒⇒ AE⊥AFAE⊥AF (tính chất hai góc kề bù)
Hay AE⊥DFAE⊥DF
d) Chứng minh tương tự câu a ta có BF là tia phân giác của ˆABCABC^
CD là tia phân giác của ˆACBACB^
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
⇒BF⊥BE⇒BF⊥BE (tính chất hai góc kề bù)
Hay BF⊥EDBF⊥ED
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
⇒CD⊥CE⇒CD⊥CE (tính chất hai góc kề bù)
Hay CD⊥EF

a) E thuộc tia phân giác của ˆCBHCBHˆ
⇒⇒ EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ˆBCKBCKˆ
⇒⇒ EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK
b) EH = EK
⇒⇒ E thuộc tia phân giác của ˆBACBACˆ mà E # A
Vậy AE là tia phân giác của ˆBACBACˆ
c) AE là tia phân giác góc trong tại đỉnh A.
AF là tia phân giác góc ngoài tại đỉnh A.
⇒⇒ AE⊥AFAE⊥AF (tính chất hai góc kề bù)
Hay AE⊥DFAE⊥DF
d) Chứng minh tương tự câu a ta có BF là tia phân giác của ˆABCABCˆ
CD là tia phân giác của ˆACBACBˆ
Vậy các đường AE, BF, CD là các đường phân giác của ∆ABC
e) BF là phân giác góc trong tại đỉnh B.
BE là phân giác góc ngoài tại đỉnh B.
⇒BF⊥BE⇒BF⊥BE (tính chất hai góc kề bù)
Hay BF⊥EDBF⊥ED
CD là đường phân giác góc trong tại C
CE là đường phân giác góc ngoài tại C
⇒CD⊥CE⇒CD⊥CE (tính chất hai góc kề bù)
Hay CD⊥EF

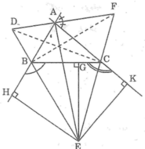
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.

a. Ta có: E thuộc tia phân giác của ∠(CBH)
Suy ra: EG = EH (tính chất tia phân giác) (1)
E thuộc tia phân giác của ∠(BCK)
Suy ra: EG = EK (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra: EH = EG = EK.
b. Ta có: EH = EK (chứng minh trên)
Suy ra: E thuộc tia phân giác của ∠(BAC).
Mà E khác A nên AE là tia phân giác của ∠(BAC)
c. Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc trong tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
d. Tương tự câu a, ta có:
BF là tia phân giác của ∠(ABC)
CD là tia phân giác của ∠(ACB)
Vậy AE, BF, CD là các đường phân giác của tam giác ABC.
e. Ta có: BF là tia phân giác góc trong tại đỉnh B
BE là tia phân giác góc trong tại đỉnh B
Suy ra: BF ⊥ BE (tính chất hai góc kề bù)
Vậy BF ⊥ ED.
Lại có: CD là đường phân giác góc trong tại C
CE là đường phân giác góc trong tại C
Suy ra: CD ⊥ CE (tính chất hai góc kề bù)
Vậy CD ⊥ EF.

Bạn tự vẽ hình nha![]()
a.
EB là tia phân giác của ABC
=> EH = EG (1)
EC là tia phân giác của ACB
=> EK = EG (2)
Từ (1) và (2)
=> EH = EG = EK
b.
EB là tia phân giác của ABC
EC là tia phân giác của ACB
=> E là giao điểm của ba đường phân giác của tam giác ABC
=> AE là tia phân giác của BAC
c.
Gọi Ax là tia đối của tia AC
xAB + BAC = 1800
xAB = 1800 - BAC
AF là tia phân giác của xAB
=> xAF = FAB = \(\frac{xAB}{2}=\frac{180^0-BAC}{2}=90^0-\frac{BAC}{2}\)
AE là tia phân giác của BAC
=> BAE = EAC = BAC/2
FAE = FAB + BAE
\(=90^0-\frac{BAC}{2}+\frac{BAC}{2}\)
= 900
=> AE _I_ DF
Chúc bạn học tốt![]()
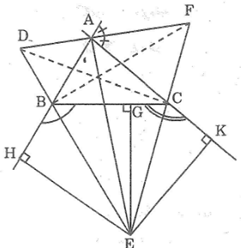
Ta có: BF là tia phân giác góc trong tại đỉnh B
BE là tia phân giác góc ngoài tại đỉnh B
Suy ra: BF ⊥ BE (tính chất hai góc kề bù)
Vậy BF ⊥ ED.
Lại có: CD là đường phân giác góc ngoài tại C
CE là đường phân giác góc trong tại C
Suy ra: CD ⊥ CE (tính chất hai góc kề bù)
Vậy CD ⊥ EF.
Vậy các đường thẳng EA; FB; DC là các đường cao trong tam giác DEF.