Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) thêm một phương trình bậc nhất hai ẩn để được hai ẩn để được một hệ có nghiệm duy nhất đó là : \(2x-3y=7\)
b) thêm một phương trình bậc nhất hai ẩn để được một hệ vô nghiệm là : \(6x-4y=11\)
c) thêm một phương trình bậc nhất hai ẩn để được một hệ có vô số nghiệm là : \(9x-6y=15\)

Ta có: 3x – 2y = 5 ⇔ 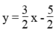
Để được một hệ có vô số nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc bằng - 5/2 .
Chẳng hạn: 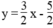 ⇔ 6x – 4y = 10
⇔ 6x – 4y = 10
Khi đó ta có hệ 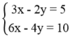 có vô số nghiệm.
có vô số nghiệm.

Ta có: 3x – 2y = 5 ⇔ 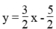
Để được một hệ có nghiệm duy nhất thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc khác 3/2 .
Chẳng hạn: 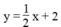 ⇔ -x + 2y = 4
⇔ -x + 2y = 4
Khi đó ta có hệ 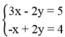 có một nghiệm duy nhất.
có một nghiệm duy nhất.

\(\hept{\begin{cases}mx+3y=-4\left(1\right)\\x-2y=5\left(2\right)\end{cases}}\)
từ \(\left(2\right)\) ta có \(x=2y+5\) \(\left(3\right)\)
thay \(\left(3\right)\)vào \(\left(1\right)\)ta có:
\(m\left(2y+5\right)+3y=-4\)
\(\Leftrightarrow2ym+5m+3y=-4\)
\(\Leftrightarrow y\left(2m+3\right)=-4-5m\) \(\left(4\right)\)
để hpt có nghiệm duy nhất thì phương trình (4) phải có nghiệm duy nhất
\(\Leftrightarrow2m+3\ne0\Leftrightarrow m\ne\frac{-3}{2}\)
từ \(\left(4\right)\) ta có: \(y=\frac{-5m-4}{2m+3}\)
từ \(\left(3\right)\)ta có: \(x=\frac{-10m-8}{2m+3}+5\)
\(\Leftrightarrow x=\frac{-10m-8+10m+15}{2m+3}\)
\(\Leftrightarrow x=\frac{7}{2m+3}\)
ta có : \(x=\frac{7}{2m+3}\)
\(\Leftrightarrow2m+3\in\left\{\pm1;\pm7\right\}\) ( tự tìm )
\(y=\frac{-5m-4}{2m+3}\)
\(y=\frac{2m+3-7m-7}{2m+3}\)
\(y=1-\frac{7m+7}{2m+3}\)
\(\Leftrightarrow2m+3\inƯ\left(7m+7\right)\)
lập bảng xét nghiệm là xong

1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)

Vì a+b+c=0 nên pt nghiệm là 1 và 2m-3
Theo đề bài ra ta phải có (2m-3)2=1 hoặc 2m-3=(-1)2
ĐS: m=1 hoặc m=2
Ta có: 3x – 2y = 5 ⇔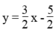
Để được một hệ vô nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc khác - 5/2 .
Chẳng hạn: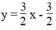 ⇔ 3x – 2y = 3
⇔ 3x – 2y = 3
Khi đó ta có hệ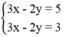 vô nghiệm.
vô nghiệm.