Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì BCD là tam giác đều nên ta có:
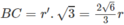
Diện tích của tam giác đều BCD là:
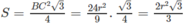
Thể tích hình chóp A.BCD là:
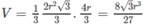
Hai hình chóp A.BCD và A’.BCD có chung mặt đáy BCD nên:
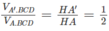
Do đó
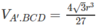

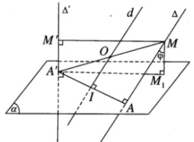
Theo giả thiết ta có: ∠A′M′M = ∠A′AM = ∠A′M1M = 90o
Do đó 5 điểm A, A’, M, M’, M1 cùng thuộc mặt cầu (S) tâm O, với O là trung điểm của A’M và có bán kính r = A′M2
Mặt khác ta có A’M2 = A’A2 + AM2
Trong đó
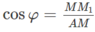
Do đó
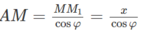
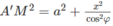
Mặt cầu tâm O có bán kính
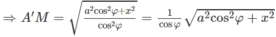
Diện tích của mặt cầu tâm O là:
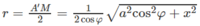

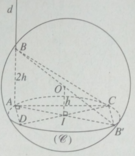
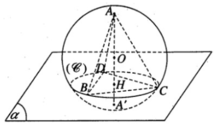
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).

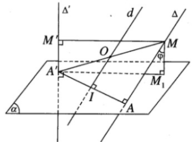
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

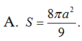
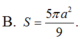
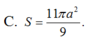
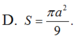
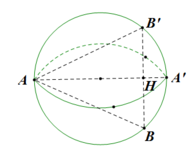

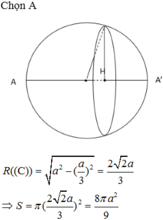




Theo giả thiết ta có AH = 4r/3
Ta suy ra OH = r/3. Gọi r’ là bán kính của đường tròn (C).
Ta có:
Vậy diện tích của hình tròn (C) là: