Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

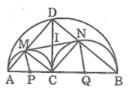
Tam giác ACD vuông tại C có CM ⊥ AD
Theo hệ thức lượng trong tam giác vuông, ta có:
C D 2 = DM.DA (1)
Tam giác BCD vuông tại C có CN ⊥ BD
Theo hệ thức lượng trong tam giác vuông, ta có:
C D 2 = DN.DB (2)
Từ (1) và (2) suy ra: DM.DA = DN.DB

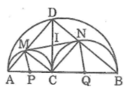
Tam giác ABD nội tiếp trong đường tròn có AB là đường kính nên ![]() = 90o hay
= 90o hay ![]() =
90
°
=
90
°
Tam giác ACM nội tiếp trong đường tròn có AC là đường kính nên ![]() =
90
°
=
90
°
Suy ra: CM ⊥ AD ⇒ ![]() =
90
°
=
90
°
Tam giác BCN nội tiếp trong đường tròn có AC là đường kính nên ![]() =
90
°
=
90
°
Suy ra: CN ⊥ BD ⇒  =
90
°
=
90
°
Tứ giác CMDN có ba góc vuông nên nó là hình chữ nhật

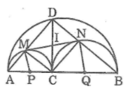
Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD = MN
Trong tam giác OCD ta có: CD ≤ OD nên MN ≤ OD
Vì OD không đổi nên MN = OD là giá trị lớn nhất khi và chỉ khi C trùng với O
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.

a: góc AMC=1/2*180=90 độ
=>góc DMC=90 độ
góc CNB=1/2*180=90 độ
=>góc DNC=90 độ
Kẻ tiếp tuyến Cx của hai đường tròn đường kính AC,CB, Cx cắt MN tại I
Xét (E) có
IC,IM là tiếp tuyến
=>IC=IM
Xét (F) có
IN,IC là tiếp tuyến
=>IN=IC=IM
Xét ΔMCN có
CI là trung tuyến
CI=MN/2
=>ΔMCN vuông tại C
góc DMC=góc DNC=góc MCN=90 độ
=>DMCN là hcn
b: ΔDCA vuông tại C có CM vừa là đường cao
nên DM*DA=DC^2
ΔDCB vuông tại C có CN là đường cao
nên DN*DB=DC^2=DM*DA

a) Xét tứ giác AOMC có
ˆCAOCAO^ và ˆCMOCMO^ là hai góc đối
ˆCAO+ˆCMO=1800(900+900=1800)CAO^+CMO^=1800(900+900=1800)
Do đó: AOMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Ta có: AOMC là tứ giác nội tiếp(cmt)
nên ˆMAO=ˆOCMMAO^=OCM^(hai góc cùng nhìn cạnh OM)
hay ˆMAB=ˆOCDMAB^=OCD^
Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(Gt)
CA là tiếp tuyến có A là tiếp điểm(Gt)
Do đó: OC là tia phân giác của ˆAOMAOM^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆAOM=2⋅ˆCOM⇔AOM^=2⋅COM^
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OD là tia phân giác của ˆMOBMOB^(Tính chất hai tiếp tuyến cắt nhau)
⇔ˆBOM=2⋅ˆMOD⇔BOM^=2⋅MOD^
Ta có: ˆAOM+ˆBOM=1800AOM^+BOM^=1800(hai góc kề bù)
mà ˆAOM=2⋅ˆCOMAOM^=2⋅COM^(cmt)
và ˆBOM=2⋅ˆMODBOM^=2⋅MOD^(cmt)
nên 2⋅ˆCOM+2⋅ˆMOD=18002⋅COM^+2⋅MOD^=1800
⇔ˆCOM+ˆMOD=900⇔COM^+MOD^=900
mà ˆCOM+ˆMOD=ˆCODCOM^+MOD^=COD^(tia OM nằm giữa hai tia OC,OD)
nên ˆCOD=900COD^=900
Xét ΔCOD có ˆCOD=900COD^=900(cmt)
nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)
Xét (O) có
ΔMAB nội tiếp đường tròn(M,A,B∈(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
Xét ΔAMB vuông tại M và ΔCOD vuông tại O có
ˆMAB=ˆOCDMAB^=OCD^(cmt)
Do đó: ΔAMB∼ΔCOD(g-g)
⇔AMCO=BMDOAMCO=BMDO(Các cặp cạnh tương ứng tỉ lệ)
hay AM⋅OD=BM⋅OCAM⋅OD=BM⋅OC(đpcm)


Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên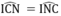 (3)
(3)
Tam giác CNQ cân tại Q nên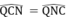 (4)
(4)
Vì AB ⊥ CD nên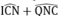 =
90
°
(5)
=
90
°
(5)
Từ (3), (4) và (5) suy ra: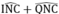 =
90
°
hay MN ⊥ QN
=
90
°
hay MN ⊥ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC
Tam giác CMI cân tại I nên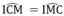 (6)
(6)
Tam giác CMP cân tại P nên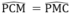 (7)
(7)
Vì AB ⊥ CD nên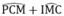 =
90
°
(8)
=
90
°
(8)
Từ (6), (7) và (8) suy ra: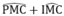 =
90
°
hay MN ⊥ PM
=
90
°
hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC