

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

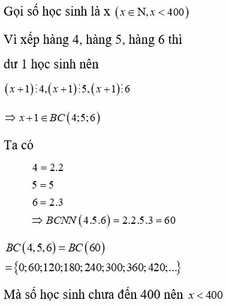


Gọi số học sinh là x (x ∈ N, x<400)
Vì xếp hàng 4, hàng 5, hàng 6 thì dư 1 học sinh nên (x+1) ⋮ 4; (x+1) ⋮ 5; (x+1) ⋮ 6
=> (x+1) ∈ BC(4;5;6)
Ta có: 4 = 2.2; 5 = 5; 6 = 2.3
=> BCNN(4;5;6) = 2.2.5.3 = 60
BC(4,5,6) = BC(60) = {0;60;120;180;240;300;360;420;...}
Mà số học sinh chưa đến 400 nên x < 400
x+1 = 0 không có x thỏa mãn.
x+1 = 60 => x = 59
x+1 = 120 => x = 119
x+1 = 180 => x = 179
x+1 = 240 => x = 239
x+1 = 300 => x = 199
x+1 = 360 => x = 359
Vì x ⋮ 7 nên x = 119 thỏa mãn.
Vậy số học sinh khối 7 là 119 học sinh

Gọi a là số học sinh
Theo đè bài ta có: a+1 thuộc BC (4,5,6) và a là số chia hết cho 7 nhỏ hơn 400
BCNN (4,5,6) = 60
BC (4,5,6) = 13 (60) = {0;60;120;180,240;300;360}
Vì a + 1 thuộc {0;60;120;.....}
a thuộc {1;61;121;181;241;301;361}
Mà a < 400 vs a chia hết cho 7
suy ra a = 301
Vậy số hs cần tìm là 301
Gọi a là số học sinh (học sinh,\(a\inℕ^∗\) )
theo đề ra ta có:
\(a⋮4\)
\(a⋮5\)
\(a⋮6\)
\(a⋮7\)
\(\Rightarrow\) a = BCNN(4;5;6;7)
ta có:
4 = 22
5 = 5
6 = 2 . 3
\(\Rightarrow\) BCNN(4;5;6;7) = 22 . 3 . 5 = 60
\(\Rightarrow\) BC(4;5;6) = B(60) ={0;60;120;180;240;300;360;...}
Vì \(a\in\) BC(4;5;6) và a < 400 nên a = {360}
Vậy a = 360

gọi số hs là x
4=2 mũ 2
5=5
6=2.3
BCNN = 60
BC của 60 ={0,60,120,180,240,300}
=>x=301
Câu trả lời của minh ko rõ mong bạn bổ sung và bỏ qua cho

Gọi số học sinh là a , ta có:
a - 1= BC (2,3,4,5,6)
2 = 2 ; 3 = 3 ; 4 = 22 ; 5 = 5 ; 6 = 2.3
=> BCNN(2,3,4,5,6) = 22.3.5 = 60
Vậy a thuộc {59 ; 119 ; 179 ; 239 ; ...}
MÀ ta thấy 119 nhỏ nhất chia hết cho 7
Vậy số học sinh là 119 học sinh

Gọi số học sinh là a thì a+1 ∈ BC(2;3;4;5); a ⋮ 7 và a < 300
Ta có BCNN(2;3;4;5) = 60
a+1 ∈ {0;60;120;180;240;300;..}
a ∈ {59;119;179;239;299;...}
Vì a ⋮ 7 và a < 300 nên a = 119