Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ai làm nhanh tớ tick. ( Quan trọng cách trình bày nhá)
1 hình tứ giác lồi có 4 đỉnh là 4 nhà máy sản xuất thép được đặt ở 4 địa điểm khác nhau tạo thành
\(\Rightarrow\) Công ty phải đặt trung tâm điều hành ở giao điểm 2 đường chéo của hình tứ giác đó

đặt ở giữa
vì (xem ảnh)
a b c d
vậy đặt ở giữa
chúc bn
hok tốt

Giúp câu 1 thôi :v
A B C S S S 1 2
Lúc 8 giờ 40 phút thì xe đi từ A đến điểm C. Gọi B là giao điểm gặp nhau của 2 xe
Trong 1 giờ 40 phút xe đi xe đạp đi được quãng đường:\(S=v_1\cdot t_1=10\cdot\frac{5}{3}=\frac{50}{3}\left(km\right)\)
Đến khi gặp nhau thì xe máy đi được quãng đường:\(S_1=v_2\cdot t_2=30.t\)
Đến khi gặp nhau thì xe đạp đi được quãng đường: \(S_2=v\cdot t=10t\)
Ta có:\(S_1-S_2=S\Leftrightarrow30t-10t=\frac{50}{3}\)
Làm nốt
Câu 1 Gọi thời gian để người đi xe máy đuổi kịp người đi xe đạp là a giờ (a>0)
Thời gian người đi xe đạp xuất phát trước xe máy là : 8h40'-7h=1h40'=5/3h
=>Quãng đường người đi xe đạp đi trước người đi xe máy là : 10.5/3=50/3(km/h)
Vì vận tốc của người đi xe máy là 30km/h , vận tốc của người đi xe đạp là 10km/h
=> cứ 1 h người đi xe máy lại đến gần người đi xe đạp một khoảng là : 30-10=20km
=> Thời gian để người đi xe máy đuổi kịp người đi xe đạp là : a=50/3 : 20 =5/6h=50'
=> Thời gian lúc 2 người gặp nhau là : 8h40' + 50'=9h30'
Vậy hai người gặp nhau lúc 9h30'
Câu 2 :
Gọi thời gian 2 người gặp nhau kể từ khi người thứ 2 xuất phát là x(h)(x>0)
Thời gian 2 người gặp nhau kể từ khi người thứ nhất xuất phát là x+1/15(h)
Khi gặp nhau :
Người thứ nhất đi được: 5,7(x+1/15) (km)
Người thứ 2 đi được: 6,3x(km)
Vì 2 người đi ngược chiều nhau và khởi hành ở 2 địa điểm cách nhau 4,18(km)
nên ta có pt: 5,7(x+1/15)+6,3x=4,18
5,7x+0,38+6,3x=4,18
⇔12x=3,8
⇔x = 1960(TMĐK)
Vậy người thứ 2 đi được 19/60(h)thì 2 người gặp nhau.

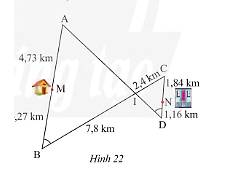
Ta có: \(AB = AM + MB = 4,73 + 4,27 = 9m\);\(CD = CN + ND = 1,84 + 1,16 = 3m\)
Xét tam giác \(AIB\) tam giác \(CID\) ta có:
\(\widehat {ABI} = \widehat {CDI}\) (giả thuyết)
\(\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh)
Do đó, \(\Delta AIB\backsim\Delta CID\) (g.g)
Suy ra, \(\frac{{AB}}{{CD}} = \frac{{AI}}{{CI}} = \frac{{BI}}{{DI}} \Leftrightarrow \frac{9}{3} = \frac{{AI}}{{2,4}} = \frac{{7,8}}{{DI}}\).
Ta có:
\(\frac{9}{3} = \frac{{AI}}{{2,4}} \Rightarrow AI = \frac{{9.2,4}}{3} = 7,2m\);\(\frac{9}{3} = \frac{{7,8}}{{ID}} \Rightarrow ID = \frac{{3.7,8}}{9} = 2,6m\).
Các con đường đi từ nhà anh Thanh đến công ty là:
Con đường: \(MB \to BI \to IC \to CN\) có độ dài là:
\(MB + BI + IC + CN = 4,27 + 7,8 + 2,4 + 1,84 = 16,31km\)
Con đường: \(MB \to BI \to ID \to DN\) có độ dài là:
\(MB + BI + ID + DN = 4,27 + 7,8 + 2,6 + 1,16 = 15,83km\)
Con đường: \(MA \to AI \to ID \to DN\) có độ dài là:
\(MA + AI + ID + DN = 4,73 + 7,2 + 2,6 + 1,16 = 15,69km\)
Con đường: \(MA \to AI \to IC \to CN\) có độ dài là:
\(MA + AI + IC + CN = 4,73 + 7,2 + 2,4 + 1,84 = 16,17km\)
Vậy đi theo con đường \(MA \to AI \to ID \to DN\) là ngắn nhất.