
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

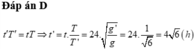

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Vật ở VTCB lò xo giãn ra một đoạn: \(\Delta l\)
\(\Rightarrow\Delta l=\frac{g}{\omega^2}\Leftrightarrow\omega\sqrt{\frac{g}{\Delta l}}\)
Tần số của con lắc lò xo:
\(\Rightarrow f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}\)

Chạy đúng: \(T=2\pi\sqrt{\dfrac{l}{g}}\)
Chạy sai: \(T'=2\pi\sqrt{\dfrac{l}{g\prime}}\), Với gia tốc trọng trường \(g'=g(\dfrac{R}{R+h})^2\)
Tỷ số: \(\dfrac{T'}{T}=\dfrac{g'}{g}=\dfrac{R}{R+h} <1\) nên đồng hồ chạy nhanh.
Một ngày đêm sẽ nhanh
\(\Delta t= 24.60.60.\mid\dfrac{T\prime}{T}-1\mid=24.60.60.\dfrac{h}{R+h}=67,45 (s)\approx68(s)\)
Bạn ơi mình chắc chắn là chạy chậm hơn vì càng cách xa mặt đất thì áp suất càng thấp quả lắc sẽ nhẹ hơn nên dao động sẽ chậm hơn. Dù sao cũng cảm ơn bạn nhiều ^^

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Khi tăng điện dung nên 2,5 lần thì dung kháng giảm 2,5 lần. Cường độ dòng trễ pha hơn hiệu điện thế \(\pi\text{/}4\) nên
\(Z_L-\frac{Z_C}{2,5}=R\)
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì
\(Z_LZ_C=R^2+Z^2_L\)
\(Z_LZ_C=\left(Z_L-\frac{Z_C}{2,5}\right)^2+Z^2_L\)
Giải phương trình bậc 2 ta được
\(Z_C=\frac{5}{4}Z_L\) hoặc \(Z_C=10Z_L\) (loại vì Zl-Zc/2.5=R<0)
\(R=\frac{Z_L}{2}\)
Vẽ giản đồ vecto ta được \(U\) vuông góc với \(U_{RL}\) còn \(U_C\) ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi \(U_L\) và \(U_{LR}\)
\(\tan\alpha=\frac{R}{Z_L}=0,5\)
\(\sin\alpha=1\text{/}\sqrt{5}\)
\(U=U_C\sin\alpha=100V\)
\(U_o=U\sqrt{2}=100\sqrt{2}V\)
chọn C
