Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Vận tốc của xe lúc bắt đầu hãm phanh
+ Ta có vận tốc; quãng đường trong chuyển động thẳng biến đổi đều
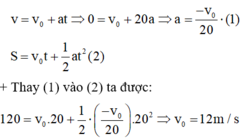
Do vậy, ta xác định được độ lớn động lượng của xe lúc bắt đầu hãm phanh bằng
p = m.v = 5000.12 = 60000 kg.m/s.

Ta có: \(s=\dfrac{1}{2}at^2=\dfrac{1}{2}a\cdot2^2\Rightarrow a=-5\left(\dfrac{m}{s^2}\right)\)
Lại có: \(v^2-v_0^2=2as\Rightarrow v_0=\sqrt{v^2-2as}\)
\(\Leftrightarrow v_0=\sqrt{0^2-2\cdot\left(-5\right)\cdot10}=10\left(\dfrac{m}{s}\right)\)
Động lượng xe lúc bắt đầu hãm phanh:
\(p=mv=5000\cdot10=50000\left(kg\cdot\dfrac{m}{s}\right)\)

1) t=20s
s =120m
v=0
v0=?; a =?
GIẢI :
Ta có : \(s=v_0t+\frac{1}{2}at^2\)
áp dụng vào bài ta có: \(120=v_0.20-\frac{1}{2}a.20^2=20v_0-200a\) (a)
lại có: \(a=\frac{0-v_0}{20}=-\frac{v_0}{20}\) (b)
Thay (b) vào (a) được: \(120=20v_0-\frac{200.\left(-v_0\right)}{20}\)
<=> \(120=20v_0+10v_0=30v_0\)
=> v0 = 4m/s
gia tốc a là :\(a=\frac{-4}{20}=-0,2\left(m/s^2\right)\)
2) v0= 20m/s
a =2m/s2
s=100m
______________________
v =?
GIẢI :
Vận tốc của xe là:
\(v^2-v_0^2=2as\)
=> \(v=\sqrt{2as+v^2_0}=\sqrt{2.2.100+20^2}=20\sqrt{2}\left(m/s\right)\)

gốc tọa độ tại A, chiều dương từ A-B, gốc thời gian lúc xe 1 bắt đầu chuyển động
a) x1=x0+v0.t+a.t2.0,5=0,2t2
x2=x0+vo.t+a.t2.0,5=560-10t+0,1t2
b) hai xe gặp nhau x1=x2\(\Rightarrow\)\(\left[{}\begin{matrix}t=40\left(n\right)\\t=-140\left(l\right)\end{matrix}\right.\)
vậy sau 40s hai xe gặp nhau
vị trí hai xe gặp nhau x1=x2=320m
ngược chiều chuyển động nên vận tốc âm còn gia tốc ban đầu là âm ngược chiều nên thành dương CDĐ

2) ta có : \(\left\{{}\begin{matrix}v_0+a\left(3-\frac{1}{2}\right)=8\\v_0+a\left(6-\frac{1}{2}\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_0+\frac{5}{2}a=8\\v_0+\frac{11}{2}a=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}-3a=6\\v_0+\frac{5}{2}a=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-2\left(m/s^2\right)\\v_0=13m/s\end{matrix}\right.\)
=> Chọn D.
Bài1:
\(S_1=v_0.2-\frac{1}{2}.a2^2=20\)
=> \(2v_0-2a=60\)(1)
\(v^2-v_0^2=2as\Rightarrow0^2-v_0^2=2a.20\Rightarrow v_0=\sqrt{40a}\)(2)
Từ (1) và (2) => \(2.\sqrt{40a}-2a=60\)
=> \(2\left(\sqrt{40a}-a\right)=60\)
<=> \(\sqrt{40a}-a=30\)
<=> \(\sqrt{40a}=30+a\Leftrightarrow40a=a^2+60a+900\)
=> \(a^2+20a+900=0\) (pt vô nghiệm)
Đáp án A.
Vận tốc của xe lúc bắt đầu hãm phanh
+ Ta có vận tốc; quãng đường trong chuyển động thẳng biến đổi đều
+ Thay (1) vào (2) ta được:
Do vậy, ta xác định được độ lớn động lượng của xe lúc bắt đầu hãm phanh bằng
p = m.v = 5000.12 = 60000 kg.m/s.