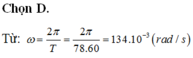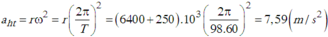Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a_{ht}=g=\frac{v^2}{R}=\frac{v^2}{\left(6400+200\right).1000}=9,2\)
=> v=?

Ta có: Fhd= Fht
\(\Rightarrow\)G=mM(R+h)2=mv2R+h
\(\Rightarrow\)G=mM(R+h)2=mv2R+h
\(\Rightarrow\)v=√mMR+h
\(\Rightarrow\)v=mMR+h khi h = R
⇒v=√GM2R
\(\Rightarrow\)v=GM2R (1)
Mặt khác do:
g=GMR2\(\Leftrightarrow\)gR2=G.MTĐg=GMR2\(\Leftrightarrow\)gR2=G.MTĐ (2)
Từ (1) và (2) ⇒v=√g.R22R=√gR2=√10.64.1052
\(\Rightarrow\)v=g.R22R=gR2=10.64.1052
\(\Rightarrow\)v=√32.106⇒v=32.106 = 5,656.103m/s
+ Chu kì \(T=\dfrac{2\pi}{\omega}\)
Mà v = ω (R + h)
\(\Rightarrow\)T=2πv(R+h)⇒T=2πv(R+h)
\(\Rightarrow\)T=2π(R+h)v=4\(\pi\)Rv
\(\Rightarrow\)T=2\(\pi\)(R+h)v=4\(\pi\)Rv
\(\Rightarrow\)T=4.3,14.6400.103/ 5,656.103
\(\Rightarrow\)T=4.3,14.6400.1035,656.103 = 14,212,16s
\(\Rightarrow\)T \(\approx\)14,212 (s)

a) chu kỳ của vệ tinh
\(T=\dfrac{2\pi}{\omega}\)\(\approx\)9666,43s
b) khoảng cách từ tâm trái đất đến vệ tinh là r=11600.103+6400.103=18.106m
tốc độ dài của vệ tinh trên quỹ đạo
v=\(\omega.r\)\(\approx\)1,7399.1011m
c) gia tốc hướng tâm của vệ tinh
aht=v2/r\(\approx\)1,68.1015m/s2

Tốc độ góc và gia tốc hướng tâm của vệ tinh được tính theo các công thức
ω = 2 π /T = (2.3.14)/(88.60) ≈ 1.19. 10 - 3 (rad/s)
a h t = ω 2 (R + h) = 1 . 19 . 10 - 3 2 .6650. 10 3 = 9,42 m/ s 2

Trọng lượng là độ lớn của trọng lực. Trọng lực trong trường hợp này ta coi như là lực hấp dẫn của vệ tinh và trái đất. Lực hấp dẫn giữ cho vệ tinh quay xung quanh trái đất đóng vai trò là lực hướng tâm. Đến đây câu a đã được giải quyết. Từ câu a ta có Fht=m.(2.pi/T)2.(RTĐ+h). Từ đây ta rút h là độ cao cần tìm.
a) Lực hướng tâm bằng lực hấp dẫn, bằng trọng lượng của vật là 920 (N)
b) Ta có:
\(F_{ht}=m.a_{ht}=m.\omega^2.(R_đ+h)=m.\dfrac{4\pi^2}{T^2}.(R+h)\)
Suy ra \(R+h\)
Với \(R=6400km\), từ đó suy ra \(h\)