Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
+ f = 1 T = ω 2 π → ω = 2 π f
+ Lực hướng tâm tác dụng vào vật: F h t = m ω 2 r = m 2 π f 2 r
+ Để vật không văng ra khỏi mặt bàn, ta phải có:
F = F m s n max ↔ m 2 π f 2 r = F m s n max → f 2 = F m s n max m 4 π 2 r = 0 , 08 20.10 − 3 .4 π 2 .1 = 0 , 101 → f ≈ 0 , 32 s − 1
Vậy muốn vật không bị văng ra khỏi mặt bàn thì tần số quay của bàn lớn nhất là: f = 0 , 32 s − 1
=> Chu kì nhỏ nhất là: T min = 1 f max = 1 32 ≈ 3,12 ( s )
Đáp án: A

Để vật không bị văng ra ngoài khỏi bàn thì: Fht ≤ Fmsn (max)
(Khi Fmsn (max) ≤ Fht thì vật bị văng)
Lực hướng tâm tác dụng vào vật:
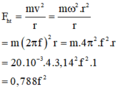
(f là tần số quay của bàn)
Để vật không bị văng ra khỏi mặt bàn ta có:
Fht ≤ Fmsn ⇔ 8.10-2. 9,8596. f2 ≤ 8.10-2
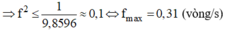

Để vật không bị văng ra khỏi bàn thì lực hướng tâm phải có giá trị bằng lực ma sát nghỉ:
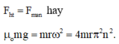
Tần số vòng lớn nhất ứng với lực ma sát nghỉ cực đại:
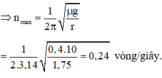
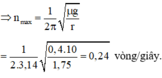

Lực ma sát nghỉ tác dụng vào vật giữ cho vật đứng yên không bị văng ra khỏi bàn quay.
Để vật không bị văng ra khỏi bàn, ta có: Fmsn(max) = Fht = = mω2r = 0,08 (N).
⇔ 𝜔=𝐹𝑚𝑠𝑛𝑚𝑎𝑥𝑚.𝑟‾‾‾‾‾‾√=0,0820.10−3.1‾‾‾‾‾‾‾√=2 (rad/s).
Vậy số vòng mà bàn quay lớn nhất là: nmax = 22𝜋≈0,318 (vòng/s).

Chọn đáp án A
Lực ma sát đóng vai trò là lực hướng tâm. Vật không bị văng ra xa tâm bàn khi
![]()
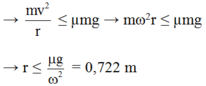

Chọn A.
Lực ma sát đóng vai trò là lực hướng tâm. Vật không bị văng ra xa tâm bàn khi F h t ≤ F m s
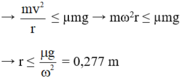

Chọn A.
Lực ma sát đóng vai trò là lực hướng tâm. Vật không bị văng ra xa tâm bàn khi Fht ≤ Fms.
![]()

Đáp án A
Lực ma sát đóng vai trò là lực hướng tâm. Vật không bị văng ra xa tâm bàn khi F h t ≤ F m s
⇒ m v 2 r ≤ μ m g ⇒ m ω 2 r ≤ μ m g ⇒ r ≤ μ g ω 2 = 0 , 272 m
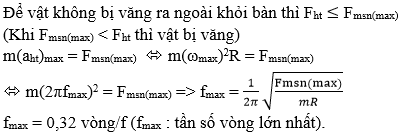
Ta có:
+ f = 1 T = ω 2 π → ω = 2 π f
+ Lực hướng tâm tác dụng vào vật: F h t = m ω 2 r = m 2 π f 2 r
+ Để vật không văng ra khỏi mặt bàn, ta phải có:
F h t = F m s n max ↔ m 2 π f 2 r = F m s n max → f 2 = F m s n max m 4 π 2 r = 0 , 08 20.10 − 3 .4 π 2 .1 = 0 , 101 → f ≈ 0 , 32 s − 1
Vậy muốn vật không bị văng ra khỏi mặt bàn thì tần số quay của bàn lớn nhất là: f = 0 , 32 s − 1
Đáp án: A