Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phải chọn 2 học sinh nam và 4 học sinh nữ ⇒ Theo quy tắc nhân số cách chọn là C 6 2 C 9 4 (Cách).

Đáp án C.
Phương pháp:
+) Chọn 2 học sinh nam.
+) Chọn 3 học sinh nữ.
+) Sử dụng quy tắc nhân.
Cách giải:
Số cách chọn 2 học sinh nam C 6 2
Số cách chọn 3 học sinh nữ C 9 3
Vậy số cách chọn 5 học sinh đi lao động trong đó có 2 học sinh nam là C 6 2 . C 9 3

Số học sinh nam khối 6 chiếm 2/9 của 3/8 số học sinh nam toàn trường, nên số học sinh nam khối 6 chiếm: (2/9)*(3/8)= 1/12 số học sinh khá giỏi bộ môn toán toàn trường.
Số học sinh nữ khối 6 chiếm 4/9 của 5/8 số học sinh nứ toàn trường, nên số học sinh nữ khối 6 chiếm: (4/9)*(5/8) = 5/18 số học sinh khá giỏi bộ môn toán toàn trường
Tổng số học sinh nam và nữ khối 6 chiếm: 1/12 + 5/18 = 13/36 số học sinh khá giỏi bộ môn toán toàn trường
Vì số học sinh khá giỏi bộ môn toán toàn trường trong khoảng từ 70 đến 100 em và là 1 số chia hết cho 36 nên số học sinh khá giỏi bộ môn toán toàn trường là 72.
Số học sinh nam khá giỏi bộ môn toán là: (1/12)*72 = 6 học sinh
Số học sinh nữ khá giỏi bộ môn toán là: (5/18)*72 = 20 học sinh

chọn đc 5 em học sinh có đúng 2 nữ vậy sẽ có 3 nam
số cách chọn đc là:\(C^2_6.C^3_8\)

Đáp án B
Số cách chọn ngẫu nhiên 1 học sinh của tổ đó đi trực nhật là: C 11 1 = 11

Đáp án B
Số cách chọn ngẫu nhiên 1 học sinh của tổ đó đi trực nhật là:
C 11 1 = 11

Ta có số tổ nhiều nhất là UWCLN(18,24) = 6
Khi đó mỗi tổ có 18 : 6 = 3 nam và 24:6 = 4 nữ


Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
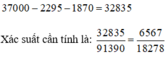
Chọn D

Đáp án B
Chọn 2 nam từ 6 nam có C 6 2 cách
Chọn 4 nữ từ 9 nữ có C 9 4 cách
Do đó có C 6 2 . C 9 4 cách thỏa mãn