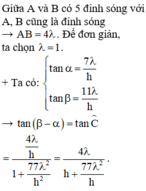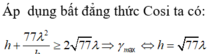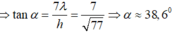Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
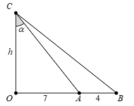
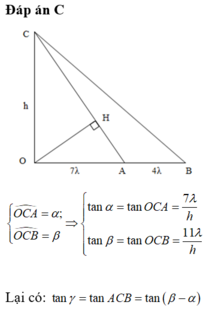
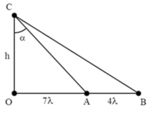
Giữa A và B có 5 đinh sóng với A, B cũng là đinh sóng → A B = 4 λ . Chuẩn hóa λ = 1
+ Ta có 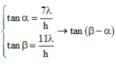
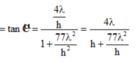
Từ biểu thức trên, ta thấy rằng góc ACB lớn nhất khi h = 77
+ Gọi M là một điểm trên AC, để M ngược pha với nguồn thì
![]()
+ Với khoảng giái trị của tính về phía C từ đường vuông góc của O lên AC: 5 . 47 ≤ d M ≤ 8 , 7 , kết hợp với chức năng Mode → 7 ta tìm được 4 vị trí.
+ Tương tự như vây ta xét đoạn về phía A: 5 , 47 ≤ d M ≤ 7 ta tìm được 2 vị trí
→ Trên AC có 6 vị trí.

Điểm M và N cách đều A,B do đó thuộc đường trung trực của AB, và đối xưng nhau qua trung điểm O của AB và OM=ON=16cm
Đường trung trực của AB là đường cực đại, các điểm trên đường này dao động với phương trình
\(x=2A\cos\left(\omega t-\frac{x}{\lambda}2\pi\right)\) x là khoảng cách từ điểm đó đến 2 nguồn
Xét từ O đến M
x sẽ nằm trong khoảng từ 12cm(AB/2) đến 20cm(pytago)
Cùng pha với nguồn
\(x=k\lambda\)
Các x thỏa mãn là 12.5; 15; 17.5 và 20
Cả hai bên sẽ có 8 (tính cả M và N)

Đáp án B
Phương pháp: Viết phương trình dao động của phần tử tại M, xét đặc điểm của pha và biên độ.
Cách giải:
Đặt phương trình dao động tại hai nguồn là: u A = u B = a cos ω t
Ta có phương trình dao động của phần tử môi trường tại M là:
u M = 2 . a . cos ( π ( d 2 - d 1 ) λ . cos ( ω t - π ( d 2 + d 1 ) λ
Do M nằm trên AB nên d2 + d1 =AB = 13λ, Thay vào phương trình ta được :
u M = 2 . a . cos ( π ( d 2 - d 1 ) λ ) . cos ( ω t - 13 π )
Vậy phần tử tại M luôn dao động ngược pha so với nguồn, cần tìm điều kiện để M cực đại:
π ( d 2 - d 1 ) λ = k 2 π ⇒ d 2 - d 1 = k 2 λ
Áp dụng điêu kiện:
- A B ≤ d 2 - d 1 ≤ A B ⇔ - 13 λ ≤ 2 k λ ≤ 13 λ ⇔ - 13 ≤ 2 k ≤ 13 ⇔ - 6 , 5 ≤ ≤ 6 , 5
Các giá trị k thỏa mãn là : k = 0; ±1; ±2…±6
Vậy có 13 điểm.