Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O u 3 a t M 2a
Điều kiện sóng dừng 2 đầu cố định: \(l=\frac{k\lambda}{2}\Rightarrow\lambda=l=\frac{v}{f}\Rightarrow f=\frac{v}{l}\)(Với k = 2, vì trên hình có 2 bụng).
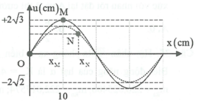
Thời gian từ \(u=x\rightarrow u=-x\) (liên tiếp): \(5\Delta t-\Delta t=4\Delta t\)
Suy ra thời gian từ vị trí: \(u=x\rightarrow u=0\) là: \(\frac{4\Delta t}{2}=2\Delta t\)
Suy ra thời gian đi từ vị trí: \(u=2a\rightarrow u=0\) (biên về VTCB) là \(\Delta t+2\Delta t=3\Delta t=\frac{T}{4}\)
Chu kì dao động: \(T=4.3\Delta t=12\Delta t\)
Suy ra: \(A_M=x=2a.\frac{\sqrt{3}}{2}=a\sqrt{3}\) (dựa vào hình vẽ, cung \(\Delta t\) ứng với 300).
Dựa vào vòng tròn: \(V_M\) \(_{max}=a\sqrt{3}.\omega=a\sqrt{3}.2\pi f=2\pi\sqrt{3}\frac{va}{l}\)
Đáp án B

Ta có $\lambda =24cm $
Bạn vẽ hình ra .
Đoạn AB =24cm sau đó vẽ 2 bụng sóng.
Lấy M N nằm giữa sao cho MN= AB/3 = 8 cm.
Khoảng cách MN lớn nhất khi chúng nằm trên bụng và nhỏ nhất khi duỗi thẳng.
Ta có $\dfrac{MN_{lớn}}{MN_{nhỏ}} =1.25 \rightarrow MN_{lớn}=10 \rightarrow $biên độ của M và N là 3cm.
Khoảng cách từ M đến nút bằng 4cm =$\dfrac{\lambda}{6} \rightarrow A_{bụng} =2\sqrt{3}$

Đây em nhé Câu hỏi của Nguyễn Thị Trúc Đào - Vật lý lớp 12 | Học trực tuyến

Sóng dừng trên dây có 2 đầu cố định thì tần số cơ bản \(f_0\) (tần số nhỏ nhất để có sóng dừng ứng với 1 bó sóng)
Thì các tần số để có sóng dừng là: \(f_n=n.f_0\)
Suy ra: \(f_0=8Hz\)
Có: \(\dfrac{1}{\lambda_{n+1}}-\dfrac{1}{\lambda_{n}}=\dfrac{f_{n+1}}{v}-\dfrac{f_{n}}{v}=\dfrac{8}{v}=0,2\Rightarrow v=40m/s\)
Tần số âm cơ bản ứng với 1 bó sóng ta có: \(l=\dfrac{\lambda}{2}=\dfrac{v}{2f_0}=\dfrac{40}{2.8}=2,5m\)
Chọn D.

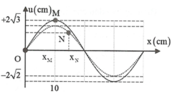
Tại thời điểm t 1 tốc độ của M là v M = ω A M 2
Tốc độ của điểm N tịa thời điểm t 2 là:
v N = ω A N 2 2
v N = v M ⇒ A N = 2 2 A M
Vậy điểm này cách nút λ 8 ⇒ x N = 15 c m
Dựa vào hình vẽ u N = 2 2 A N = A M 2 = 2 c m
Chọn đáp án C

Chọn đáp án C.
Tại thời điểm t 1 tốc độ của M là v M = ω A M 2
Tốc độ của điểm N tịa thời điểm t 2 là:
v N = ω A N 2 2
v N = v M ⇒ A N = 2 2 A M
Vậy điểm này cách nút λ 8 ⇒ x N = 15 c m
Dựa vào hình vẽ u N = 2 2 A N = A M 2 = 2 c m



Đáp án A
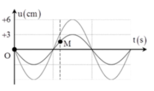
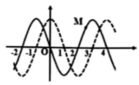
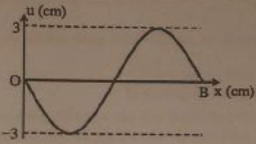
+ Từ đồ thị, ta thấy rằng điểm M dao động với biên độ bằng một nửa biên độ bụng A M = 3 c m
+ Khi hình ảnh sợi dây là đường liền nét, ta xét một điểm bụng có li độ u = 3 cm=0,5Ab → khoảng thời gian ngắn nhất để điểm bụng này quay lại li độ này sẽ là
+ Điểm M tại thời điểm t 1 đang ở vị trí biên, thời điểm t 2 = t 1 + 1 15 s tương ứng với góc quét ∆ φ = ω ∆ t = 2 π 3
tại t 2 M có li độ