Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S_1+S_2=45\) (km)
\(\Leftrightarrow v_1\frac{1,5}{2}+\frac{2}{3}v_1\frac{1,5}{2}=45\Rightarrow v_1=10,4\left(\frac{km}{gi\text{ờ}}\right)\Rightarrow v_2=6,9\left(\frac{km}{gi\text{ờ}}\right)\)

Tóm tắt :
s = 45km
\(\frac{t}{2};v_1\)
\(\frac{t}{2};v_2=\frac{2}{3}v_1\)
_____________________
v1 =?; v2 =? (t=1h30' =1,5h)
GIẢI :
Vận tốc trung bình trên cả quãng đường là :
\(v_{tb}=\frac{45}{1,5}=30\left(km/h\right)\)
Có : \(v_{tb}=\frac{s_1+s_2}{t_1+t_2}\)
<=> \(v_{tb}=\frac{v_1t_1+v_2t_2}{t_1+t_2}=\frac{\frac{t}{2v_1}+\frac{t}{2v_2}}{t}=\frac{1}{2v_1}+\frac{1}{2v_2}\)
mà: \(v_2=\frac{2}{3}v_1\)
=> \(30=\frac{1}{2v_1}+\frac{1}{\frac{4}{3}v_1}\)
\(\Leftrightarrow30=\frac{\frac{4}{3}v_1+2v_1}{\frac{8}{3}v_1^2}=\frac{\frac{10}{3}}{\frac{8}{3}v_1}=\frac{5}{4}v_1\)
=> \(\left\{{}\begin{matrix}v_1=24km/h\\v_2=\frac{2}{3}.24=16km/h\end{matrix}\right.\)

a, Gọi thời gian xe đi trên cả guãng đường là t(h)
Quãng đường xe đi được trong nửa thời gian đầu là:
S1=1/2.t.v1=1/2.t.60=t.30(km)
Quãng đường xe đi được trong nửa thời gian sau là:
S2=1/2.t.v2=1/2.t.18=t.9(km)
Vận tốc trung bình của xe trên cả quãng đường là:
vtb=(S1+S2)/t=(30t+9t)/t=39(km/h)
b, Gọi chiều dài quãng đường là S(km)
Thời gian để xe đi quãng nửa quãng đường đầu là:
t1=1/2.S/v1=1/2.S/12=S/24(h)
Thời gian để xe đi nửa quãng đường sau là:
t2=1/2.S/v2=1/2.S/12=s/24(km/h)
Vận tốc trung bình của xe trên cả quãng đường là:
vtb=S/(t1+t2)=S(S/24+S/24)=S/[S(1/24+1/24)]=12(km/h)
c, Gọi S là chiều dài quãng đường AB t là thời gian xe đi hết nửa guãng đường sau
Thời gian xe đi hết nửa quãng đường đầu là:
t1=1/2.S:60=S/120(h)
Quãng đường xe đi được trong thời gian t là:
S'=1/2.t.40+1/2.t.20=20.t+10.t=30.t(km)
Ta có S'=1/2S=>S=60.t
Vận tốc trùng bình của xe là:
vtb=S/(t1+t)=60.t/[(60.t)/120+t]=60.t/(t/2+t)=60.t/1,5t=40(km/h)

b, Thời gian xe 1 đi hết quảng đường:
\(t_1=\frac{S}{2}\left(\frac{1}{V_1}+\frac{1}{V_2}\right)\)
Thời gian 2 xe đi hết quảng đường:
\(s=\left(v_1+v_2\right)\frac{t_2}{2}\)
\(\Rightarrow t_2=\frac{2S}{v_1+v_2}\)
Xét hiệu: \(\Delta t=t_2-t_1=\frac{2S}{v_1+v_2}-\frac{s}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)\)
\(=\frac{-S\left(v_1-v_2\right)^2}{2\left(v_1+v_2\right)v_1v_2}\)
- Nếu \(v_1=v_2\) thì \(\Delta t=0\) : Hai xe đến nơi cùng lúc.
- Nếu \(v_1\ne v_2\) thì \(\Delta t< 0\) : Xe 2 đến nơi trước xe 1.

Nửa quãng đường dài là :
S=\(\frac{AB}{2}=\frac{12}{2}=6\left(km\right)\)
Thời gian xe đi trong nửa quãng đường đầu là :
t1=\(\frac{S}{v_1}=\frac{6}{v_1}\left(h\right)\)
Thời gian xe đi trong nửa quãng đường sau là :
t2=\(\frac{S}{v_2}=\frac{6}{\frac{1}{2}v_1}=\frac{12}{v_1}\left(h\right)\)
Ta có : t1+t2=t
\(\Rightarrow\frac{6}{v_1}+\frac{12}{v_1}=0,5\left(h\right)\)
\(\Rightarrow\frac{18}{v_1}=0,5\)
\(\Rightarrow v_1=36\)(km/h)
\(\Rightarrow v_2=\frac{1}{2}.v_1=\frac{1}{2}.36=18\)(km/h)

Thời gian xe đi hết quãng đường là: \(t=\dfrac{135}{45}=3\left(h\right)\)
Quãng đường xe đi nửa thời gian đầu là: \(s_1=50.\dfrac{3}{2}=75\left(km\right)\)
Quãng đường xe đi nửa thời gian sau là:
\(s_2=135-75=45\left(km\right)\)
Vận tốc xe đi nửa thời gian sau là:
\(v=\dfrac{45.2}{3}=30\left(km\h\right)\)
Gọi :
+t là thời gian đi nữa quãng đường
+v1 là vận tốc đi nửa quãng đường đầu
+v2 là vận tốc đi nửa quãng đường sau
Vận tốc TB trên cả quãng đường là:
\(v_{tb}=\dfrac{v_1.t+v_2.t}{2.t}=\dfrac{v_1+v_2}{2}\left(\dfrac{km}{h}\right)\) (*)
Thay vTB=45(km/h) và v1 =50(km/h) vào (*)
có\(45=\dfrac{50+v_2}{2}\left(\dfrac{km}{h}\right)\Rightarrow v_2=45.2-50=40\left(\dfrac{km}{h}\right)\)
Vậy vận tốc ô tô trong nửa thời gian sau 40(km/h)
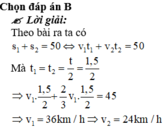


Giải: Theo bài ra ta có
s 1 + s 2 = 50 ⇔ v 1 t 1 + v 2 t 2 = 50
Mà t 1 = t 2 = t 2 = 1 , 5 2
⇒ v 1 . 1 , 5 2 + 2 3 v 1 . 1 , 5 2 = 45 ⇒ v 1 = 36 k m / h ⇒ v 2 = 24 k m / h