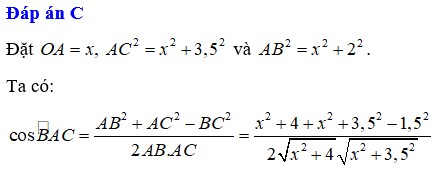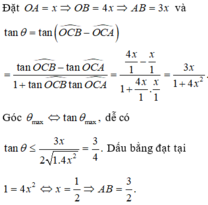Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp giải: Dựa vào hệ thức lượng trong tam giác và công thức lượng giác xác định độ lớn của góc cần tính thông qua khoảng cách. Khảo sát hàm số tìm min – max
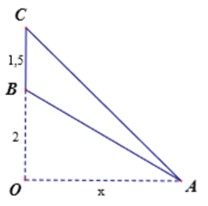
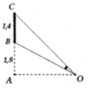
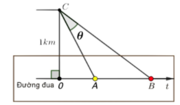
Lời giải: Với bài toán này, ta cần xác định OA để góc BOC lớn nhất. Điều này xảy ra khi tan BOC lớn nhất.
Đặt OA = x(m) với x > 0. Ta có:
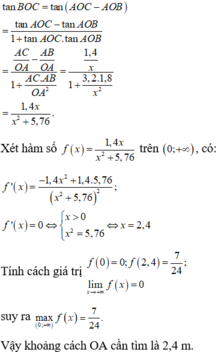

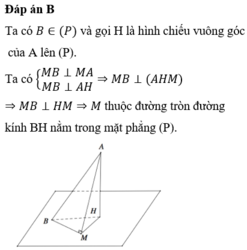
Đáp án B
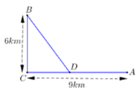
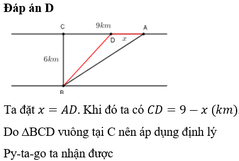
Đặt A D = x → C D = 9 − x suy ra B D = 9 − x 2 + 36 km
Chi phí lắp đặt trên đoạn AD (trên bờ) là T 1 = 100 x triệu đồng
Chi phí lắp đặt trên đoạn DB (dưới nước) là T 2 = 260 9 − x 2 + 36 triệu đồng
Vậy tổng chi phí cần tính là T = T 1 + T 2 = 100 x + 260 9 − x 2 + 36 → f x
Xét hàm số f x = 100 x + 260 x 2 − 18 x + 117 trên đoạn 0 ; 9 → min 0 ; 9 f x = 2340
Dấu = xảy ra khi và chỉ khi x = 13 2 = 6 , 5 km

Chọn đáp án B
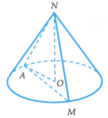
Gọi l l > 0 là độ dài đường sinh của hình nón. Vi góc ở đình bằng 120 0 nên A N O ⏜ = 60 0
Bán kính đường tròn đáy là
R = O A = N A . sin A N O ⏜ = l 3 2
Vì hình nón có góc ở đỉnh bằng 120 0 nên
![]()
Suy ra
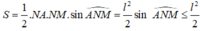
Dấu “=” xảy ra khi và chỉ khi
![]()
khi đó ∆ A N M vuông cân tại N ⇒ A M = l 2
Do A cố định nên M nằm trên đường tròn A ; l 2
Mặt khác M thuộc đường tròn đáy 0 ; l 3 2 nên M là giao điểm của đường tròn A ; l 2 và đường tròn 0 ; l 3 2
Vậy có hai vị trí của điểm M

TỰ VẼ HÌNH NHA BN :
a)Áp dụng định lí PY-ta-go vào tam giác uông ABC có:
BC^2=AB^2+AC^2
BC^2=6^2+8^2
BC^2=36+64
BC^2=100
BC^2=\(\sqrt{100}\)=>BC=10cm
Các bạn làm câu b,c,d giúp mình đi câu a mình tụ làm đc rùi