Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

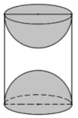
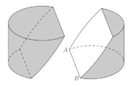
Khối cầu khoét đi có đường tròn lớn trùng với đáy hình trụ nên hai khối cầu có bán kính bằng bán kính trụ và bằng 1.
Thể tích khối trụ ban đầu là V = 1 2 . π . 2 = 2 π
Thể tích phần khoét đi là 2 nửa bán cầu, tức là 1 khối cầu có bán kính 1, có thể tích là
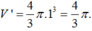
Thể tích phần còn lại của khối gỗ là
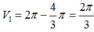
Vậy tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là
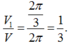
Chọn C.

Đáp án A
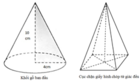
Chu vi đường tròn C = 2 π r ⇒ 2 π r = 14 c m ⇒ r = 7 c m
Xét khối món có thể tích V = 1 3 π r 2 h = 343 3 π c m 3 ⇒ h = 7 c m
Khối cầu được almf từ khối nón có bán kính mặt cầu lớn nhất khi khối cầu nội tiếp khối nón
Khi đó bán kính khối cầu (S) là R S = r . h r + r 2 + h 2 = 7 − 1 + 2 c m
Vậy diện tích lớn nhất cần tính là:
S = 4 π R 2 = 196 π 3 − 2 2 c m 2

Đáp án A.
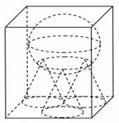
Gọi I là tâm của đường tròn dáy của chỏm cầu. M là 1 đỉnh của hình hộp thuộc đường tròn I ; R 2 .
Ta có:
I M = R 2 ; O M = R ⇒ O I = R 2 − R 2 4 = 3 R 2 .
Do đó khối hộp có chiều cao là
h = 3 R = 10 3 .
Thể tích của chỏm cầu bị cắt:
V = ∫ h 2 R π R 2 − x 2 d x = ∫ 5 3 10 π 100 − x 2 d x ≃ 53 , 87.
Thể tích của khối hộp chữ nhật:
V = S d . h = R 2 2 . 3 . R = 3 2 R 3 ≃ 866 , 025.
Thể tích khối cầu ban đầu:
V = 4 3 π R 3 ≃ 4188 , 79.
Do đó thể tích cần tính:
V ≃ 4188 , 79 − 866 , 025 − 2.53 , 87 ≃ 3215 , 023.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

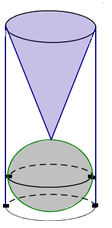
Đáp án B
Gọi R,h lần lượt là bán kính đáy và chiều cao của khối trụ ⇒ h = 6 R = 6 . Thể tích của khối trụ là V = πR 2 h = π . 1 2 . 6 = 6 π . Khối cầu bên trong khối trụ có bán kính là R = 1 ⇒ V C = 4 3 π . R 3 = 4 3 π . Khối nón bên trong khối trụ có bán kính đáy là R = 1 và chiều cao h - 2R = 4. Suy ra thể tích khối nón là V N = 1 3 πR 2 h = 1 3 . π . 1 2 . 4 = 4 3 π . Do đó, thể tích lượng nước còn lại bên trong khối trụ là V 0 = V - V C + V N = 6 π - 2 . 4 π 3 = 10 π 3 . Vậy tỉ số cần tính là T = V 0 V = 10 π 3 : 6 π = 5 9 .

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b




Chọn đáp án C.