Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Một hình cầu có số đo diện tích (đơn vị: m2) bằng số đo thể tích (đơn vị: m3). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.
Hướng dẫn làm bài:
Gọi R là bán kính hình cầu (đơn vị : mét)
Khi đó ta có: S = 4πR2 và V=4/3 πR3
Theo đề bài ta có: 4πR2=4/3πR3⇒R/3=1⇒R=3(m)
Ta có: S = 4πR2 = 4π . 32 = 36π (m2)
V=4/3 π R3=4/3 π.33=36π(m3)

Phan Minh Anh
Gọi R là bán kính hình cầu (đơn vị : mét)
Khi đó ta có: S = 4πR2 và V=43πR3V=43πR3
Theo đề bài ta có: 4πR2=43πR3⇒R3=1⇒R=3(m)4πR2=43πR3⇒R3=1⇒R=3(m)
Ta có: S = 4πR2 = 4π . 32 = 36π (m2)
V=43πR3=43π.33=36π(m3)V=43πR3=43π.33=36π(m3)
Chú ý : Một hình cầu có số đo diện tích (đơn vị: m2) bằng số đo thể tích (đơn vị: m3). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.
Sorry nha diện tích mặt cầu chứ ko phải là diện tích hình cầu.

a) Diện tích xung quanh của hình trụ : \(288\pi\left(cm^2\right)\)
b) Thể tích hình cầu : \(2304\pi\left(cm^3\right)\)
c) Diện tích mặt cầu : \(576\pi\left(cm^2\right)\)

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)


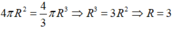
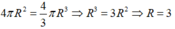
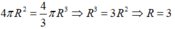
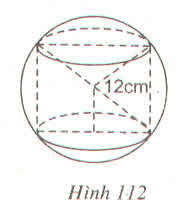
Tính được R = 3cm