

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


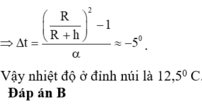

Đáp án A
Con lắc chịu hai sự biến đổi: sự nở dài về nhiệt và sự thay đổi độ cao.
Ta có:
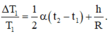
Theo đề bài, đồng hồ chạy đúng giờ nên

Suy ra
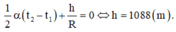

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Chọn D
Chu kì của con lắc ở mặt đất là: T = 2 π l g với g = G M R 2
Chu kì của con lắc ở độ cao h là T’: T’ = 2 π l g h với gh = G M ( R + h ) 2
Lập tỷ lệ: T ' T = g g h = R + h R = 1 + h R > 1 ⇒ T ' > T Þ Đồng hồ chạy chậm hơn so với ở mặt đất
Mỗi chu kì đồng hồ sai thời gian ΔT:
∆ T T 1 = T 2 - T 1 T 1 = h R ⇒ ∆ T = T 1 h R
Do ΔT > 0 đồng hồ chạy chậm và mỗi ngày chậm:
ζ = n . ∆ T = 24 . 3600 T 1 . T 1 . 0 , 64 6400 = 86400 . 10 - 4 = 8 , 64 ( s )

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Dùng bảo toàn cơ năng lớp 10! đề không sai !
Với biên độ góc là 600 vẽ hình sẽ thấy độ cao
Nên:

Chọn A
+ Đồng hồ chạy đúng khi tổng các sai lệch về chu kỳ bằng 0:
![]()
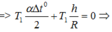
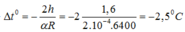
=>![]()

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Theo giả thiết thì hai bản tụ đặt thẳng đứng trái dấu, nên ta có hình sau:
+ + + + + - - - - - α E P F T
Góc lệch ở VTCB: \(\tan\alpha=\frac{F}{P}=\frac{qE}{mg}=\frac{qU}{mgd}=\frac{10^{-5}.400}{0,01.10.0,1}=0,4\)
\(\Rightarrow\alpha=21,8^0\)