Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố học sinh chỉ chọn đúng đáp án của 25 câu hỏi
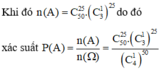

Đáp án B.
+ Rút ra 4 câu bất kì =>Có C 50 4 cách.
+ Rút ra 4 câu mà không có câu nào học thuộc =>Có C 30 4 cách.
Xác suất để bạn đó rút được 4 câu trong đó có ít nhất một câu đã học là 1 − C 30 4 C 50 4

Đáp án A
Ta xét 2 trường hợp:
TH1: Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được ⇒ P 1 = C 25 9 . C 5 1 C 30 10
TH2: Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được ⇒ P 2 = C 25 10 C 30 10
Vậy xác suất cần tính là P = P 1 + P 2 = 0 , 449

Số phần tử của không gian mẫu là n Ω = C 30 5 = 142506
Gọi A là biến cố: “đề thi lấy ra là một đề thi tốt”.
Vì trong một đề thi “tốt” có cả ba câu dễ, trung bình và khó đồng thời số câu dễ không ít hơn 2 nên ta xét các trường hợp sau:
Trường hợp 1: Đề thi gồm 3 câu dễ, 1 câu trung bình và 1 câu khó có C 15 1 C 10 1 C 5 1 cách.
Trường hợp 2: Đề thi gồm 2 câu dễ, 2 câu trung bình và 1 câu khó có C 15 2 C 10 2 C 5 1 cách.
Trường hợp 3: Đề thi gồm 2 câu dễ, 1 câu trung bình và 2 câu khó có C 15 2 C 10 1 C 5 2 cách.
Suy ra n A = C 15 3 C 10 1 C 5 1 + C 15 2 C 10 2 C 5 1 + C 15 2 C 10 1 C 5 2 = 56875
Vậy xác suất cần tìm là P A = n A n Ω = 56875 142506 = 625 1566
Đáp án D

Đáp án D
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là 3 4 . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 1 4 25 . 3 4 25




Đáp án B
Gọi A là biến cố “Rút được đề thi có 4 câu đã học thuộc”, ta lần lượt có
Vì ngân hàng câu hỏi có 100 câu và mỗi đề thi có 5 câu nên có