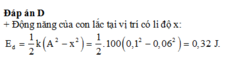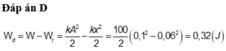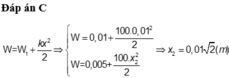Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

W d = W - W t = 1 2 m ω 2 ( A 2 - x 2 ) = 1 2 k ( A 2 - x 2 ) = 0 , 32 J. Chọn B.

W=\(\frac{1}{2}\).k.A2=0,5.100.0,12=0,5J
Wt=\(\frac{1}{2}\).k.x2=0,5.100.0,062=0,18J
Wđ =0,5-0,18=0,32J

Đáp án A
Phương pháp: Áp dụng định luật bảo toàn cơ năng
Cách giải:
Ta có
![]()
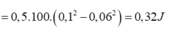

Đáp án B
Cơ năng của con lắc ![]()
Khi vật nặng cách biên 4 cm thì li độ x = 6 cm → thế năng tại vị trí này là

Bảo toàn cơ năng
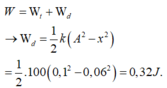

Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)

Một con lắc lò xo dao động theo phương trình x = 4cos10t
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}m.w^2.A^2=8.10^{-3}=8\left(mJ\right)\)
Vậy C đúng
Thế năng cực đại của con lắc lò xo:
\(W_t=W=\frac{1}{2}k.A^2=\frac{1}{2}.m.\omega^2.A^2=8.10^{-3}=8mJ\)
Chọn C