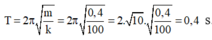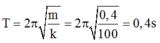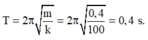Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Sử dụng công thức tính chu kì dao động của con lắc lò xo
Ta có: T = 2 π m k = 2 π 0 , 4 100 = 0 , 4 π ( s )

\(f=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}=\frac{1}{2\pi}\sqrt{\frac{\pi^2}{0.16}}=1.25Hz\)

Ta có: \(\omega=2\pi f=5\pi\) ; A = 4cm
\(\omega=\sqrt{\frac{K}{m}}=\sqrt{\frac{K}{0,1}}\Rightarrow K=25\)
\(\Delta l_o=\frac{mg}{k}=\frac{0,1.10}{25}=4cm\)
Áp dụng CT: \(F_{đh}max=K\left(\Delta l_o+A\right)\) và \(F_{đh}min=k\left(\Delta l_o-A\right)\)
Suy ra, Fmax = 2 N và Fmin = 0 N
Theo mình là đáp án khác.


T=0.4s => denta l=4 cm
thời gian dãn gấp 2 lần thời gian nén nên tnen = T/3
nếu chọn chiều (+) hướng xuống thì vị trí mà lo xo dãn là từ 2pi/3 -> 4pi/3
nên A = 8 cm

Đáp án A
Phương pháp: Áp dụng công thức tính chu kì dao động của con lắc lò xo
Cách giải:
Chu kì dao động
T = 2 π m k = 2 π 0 , 4 100 = 2 π . 0 , 2 . 0 , 4 10 = 0 , 4 . π . 1 π = 0 , 4 ( s )