Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ ĐK đầu bài ta có:
tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

Độ giãn của lò xo tại VTCB: \(\Delta l_0=\frac{9}{\omega^2}=2cm\)
Lực đàn hồi có độ lớn 1,5 N
\(F=k.\left(\Delta l\pm x\right)\Leftrightarrow1,5=50.\left(0,02\pm x\right)\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=1cm\\x=-1cm\end{array}\right.\)
Khoảng thời gian ngắn nhất vật đi qua hai vị trí mà lực đàn hồi F = 1,5 N là :
\(t=\frac{T}{12}+\frac{T}{12}=\frac{\pi}{30\sqrt{5}}=s\)
Đáp án C

Chu kì dao động: \(T=2\pi/\omega=\pi/10(s)\)
Trong thời gian \(\pi/10\)s đầu tiên bằng đúng 1 chu kì, nên quãng đường đi được là 4A = 4.6=24 cm.

Chọn đáp án B
Phương trình dao động: α = 0 , 1 cos 10 t + 0 , 79 r a d
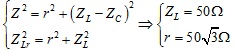
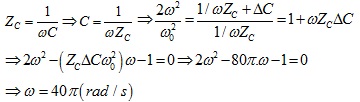

 =2 7,1 cm/s
=2 7,1 cm/s
Đáp án B
HD: Tần số góc của dao động 20 rad/s