Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Li độ dài ban đầu của nó là:
$x=\alpha.l=2$cm
Có: $\omega^2=\frac{g}{l}$
Áp dụng công thức liên hệ giữa li độ và vận tốc trong dao động điều hoà ta có:
$A^2=x^2+\frac{v^2}{\omega^2}$
$\Rightarrow A=2\sqrt2$cm

Đáp án C
+ Khi lực cân bằng trọng lượng, ta có: 3mgcos α - 2mgcos α = mg ⇒ 3 cos α - 2 cos 45 0 = 1
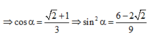
- Gia tốc tiếp tuyến:
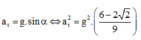
- Gia tốc hướng tâm: 2 g ( cos α - cos α 0 )
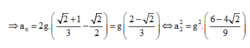
Gia tốc của vật
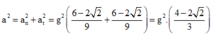
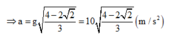

Chọn D
Biểu thức của lực căng dây: T = mg (3cosα – 2cosαo).
Với T = P = mg => ![]()
+ Gia tốc của vật: ![]()
với an là gia tốc hướng tâm và at là gia tốc tiếp tuyến.
![]()
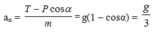
![]()

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)


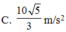
Chọn đáp án D