

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(V=1.800.000\left(l\right)=1800m^3=S.h\Rightarrow S=\frac{V}{h}=60\left(m^2\right)\)

10cm A H B O
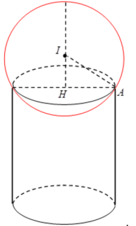
Giả sử căt hình đó thành 1 mặt phẳng đi qua trục của nón ta được thiết diện như hình vẽ. Trong đó tam giác ABC là tam giác đều và là thiết diện của khối nón. Hình tròn tâm I là thiết diện của quả bóng.
Ta nhận thấy tam giác ABC ngoại tiếp đường tròn tâm I
Hình nón có chiều cao là \(OH=3IH=30\) (cm)
Bán kính đáy nón là \(HA=\frac{30}{\sqrt{3}}=10\sqrt{3}\left(cm\right)\)
Thể tích khối nón là \(V_1=\frac{1}{3}OH.\pi.AH^2=\frac{1}{3}.30\pi.300=3000\pi\left(cm^3\right)\)
Thể tích phần không gian bên trong khối nón không bị quả bóng chiếm chỗ là :
\(V_2=\frac{1}{3}OH.\pi.AH^2-\frac{1}{4}\pi.IH^2=3000\pi-\frac{4000}{3}\pi=\frac{5000}{3}\pi\left(cm^3\right)\)

Em chỉ cần chú ý là bán \(\dfrac{1}{2}\) số còn lại mà đang còn dư 18 lít thì số còn lại sau khi bán một nửa là 36 lít. Từ đó suy ra cả thùng chưa bán có tất cả 72 lít

a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)