Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
ω = 100 2 vòng/s = 50.2π rad/s = 100π rad/s;
Bán kính quỹ đạo của một điểm trên vành bánh xe : R = 60 cm = 0,6 m.
![]()

1.Bánh xe quay đều 100 vòng trong thời gian 2s\(\Rightarrow\) \(f=\dfrac{2}{100}=0,02\)vòng/s
Tần số quay của bánh xe: \(f=50\) vòng/s
Chu kì quay: \(T=\dfrac{1}{f}=\dfrac{1}{50}s\)
2.Vận tốc góc của 1 điểm trên vành bánh xe: \(\omega=\dfrac{2\pi}{T}=100\pi\) rad/s
Vận tốc dài của 1 điểm trên vành bánh xe: \(v=\omega.r=100\pi.0,6=60\pi\) m/s
3. Gia tốc hướng tâm của 1 điểm trên vành bánh xe:
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(60\pi\right)^2}{0,6}\approx59217,63\) m/s2

2) ta có : \(\left\{{}\begin{matrix}v_0+a\left(3-\frac{1}{2}\right)=8\\v_0+a\left(6-\frac{1}{2}\right)=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_0+\frac{5}{2}a=8\\v_0+\frac{11}{2}a=2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}-3a=6\\v_0+\frac{5}{2}a=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-2\left(m/s^2\right)\\v_0=13m/s\end{matrix}\right.\)
=> Chọn D.
Bài1:
\(S_1=v_0.2-\frac{1}{2}.a2^2=20\)
=> \(2v_0-2a=60\)(1)
\(v^2-v_0^2=2as\Rightarrow0^2-v_0^2=2a.20\Rightarrow v_0=\sqrt{40a}\)(2)
Từ (1) và (2) => \(2.\sqrt{40a}-2a=60\)
=> \(2\left(\sqrt{40a}-a\right)=60\)
<=> \(\sqrt{40a}-a=30\)
<=> \(\sqrt{40a}=30+a\Leftrightarrow40a=a^2+60a+900\)
=> \(a^2+20a+900=0\) (pt vô nghiệm)

Khi bánh xe quay được một vòng thì xe đi được quãng đường bằng chu vi của bánh xe. Quãng đường mà một vòng đi được là chu vi của vòng tròn:
S = C = 2πR = 2. 3,14. 0,3 = 1,884m.
Vậy để đi được 1 km = 1000m thì bánh xe phải quay
\(N=\frac{1000}{1,884}=530,8\) vòng

a) Gọi m là khối lượng hàng hóa trên xe.
Theo đề bài, ta có: \(F=0,3\times1500=450N\)
lại có \(F=0,2\times\left(m+1500\right)\)= 450
giải phương trình trên, ta được m = 750 kg
==> Vậy khối lượng hàng hóa trên xe là 750 kg
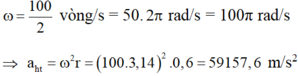
Chọn A
ω = 100 2 vòng/s = 50.2π rad/s
= 100π rad/s
Bán kính quỹ đạo của một điểm trên vành bánh xe
R = 60 cm = 0,6 m.
α h t = ω 2 R = 100 . 3 , 14 2 . 0 , 6
= 59157,6 m/s2.