Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Thể tích của khối nón là V n = 1 3 π r 2 h 1 và độ dài đường sinh là l = r 2 + h 2
Thể tích của khối trụ là V t = π r 2 h 2 = 1 3 π r 2 h
Vậy thể tích cái nắp là V = V n + V t = 2 3 π r 2 h
Mặt khác l =1,25
⇒ r 2 + h 2 = 25 4 ⇔ r 2 = 25 4 − h 2
khi đó:
V = 2 3 π h 25 4 − h 2 ≤ 2 π 3 . 125 12 3
Ta có:
V 2 = 4 9 π 2 h 2 25 4 − h 2 2 ≤ 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 ≤ 2 π 2 9 . 25 4 + 25 4 3 3
Dấu bằng xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3
Dấu “=” xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3 ⇒ r = 25 4 − h 2 = 5 6 6 ⇒ r + h ≃ 348 c m

Đáp án D
Gọi r;h lần lượt là bán kính đáy và chiều cao của khối nón ⇒ V N = 1 3 π r 2 h
Mà h = l 2 − r 2 = R 2 − r 2 = 81 − r 2 Suy ra V N = 1 3 π r 2 81 − r 2 = π 3 r 4 81 − r 2
Ta có r 2 . r 2 . 162 − 2 r 2 2 ≤ r 2 + r 2 + 162 − 2 r 2 3 2.27 = 78732 ⇒ V ≤ π 3 . 78732 ⇒ V max = 78732 3 π
Dấu " = " xaye ra ⇔ 3 r 2 = 162 ⇔ r = 3 6 ⇒ Độ dài cung tròn là l = 2 π r = 6 π 6

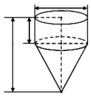
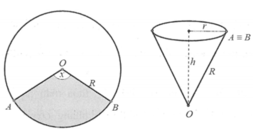
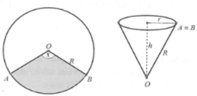
Thể tích cái phễu là V = 1 3 πr 2 h
Ta có chu vi đáy là 2 πr = Rx
Suy ra
r = R x 2 π h = R 2 - r 2 = R 2 - R 2 x 2 4 π 2 = R 2 π 4 π 2 - x 2
Áp dụng bất đẳng thức AM-GM cho 2 số dương ta có:
V = 3 R 3 48 π 2 x 2 . 2 3 π 4 π 2 - x 2 ≤ 3 R 3 2 . 48 π 2 x 2 4 3 π 2 + 4 π 2 - x 2 = 3 R 3 2 . 48 π 2 x 2 16 3 π 2 - x 2 ≤ 1 8 3 R 3 48 π 2 . x 2 + 16 3 π 2 - x 2 2 = 1 8 3 R 3 48 π 2 . 16 2 9 π 4 = 2 3 27 πR 3
Dấu bằng có khi và chỉ khi
2 3 π = 4 π 2 - x 2 x 2 = 16 3 π 2 - x 2 ⇔ x = 2 2 3 π
Vậy 2 3 27 πR 3 khi và chỉ khi x = 2 2 3 πR 3
Đáp án A

Đáp án A.
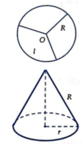
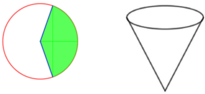
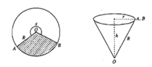
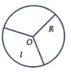
Gọi hình nón tạo thành có bán kính là r
Chu vi đáy là 2 π r = 1 3 .2 π R (bằng 1 3 chu vi của hình tròn đầu) ⇒ r = 1 3 R
Hình nón có đường sinh là R => Chiều cao
h = R 2 − r 2 = R 2 − R 2 9 = 2 R 2 3
Thể tích khối nón tạo thành là
V = 1 3 π r 2 h = 1 3 . π . R 2 9 . 2 R 2 3 = 2 R 3 π 2 81


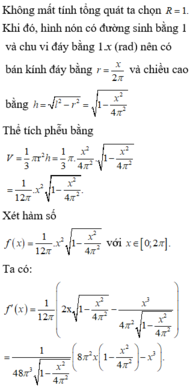

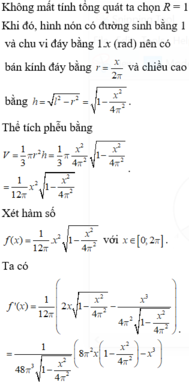


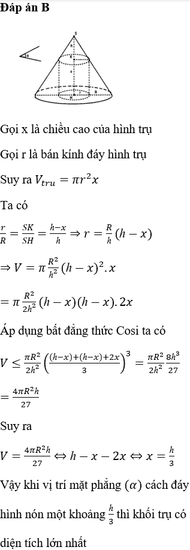

Đáp án C
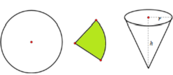
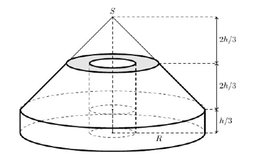
Ta có x = k . R là chu vi đường tròn đáy của khối nón ⇒ k . R = 2 π r ⇒ r = k . R 2 π
Độ dài đường sinh của khối nón chính là bán kính R ⇒ l = R = r 2 + h 2 ⇒ h = R 2 − r 2
Thể tích của khối nón là:
V = 1 3 π r 2 h = 1 3 π . r 2 . R 2 − r 2 ⇔ V 2 = π 2 9 . r 4 . R 2 − r 2 . 1
Theo bất đẳng thức Cosi, ta được r 2 . R 2 − r 2 = 4. r 2 2 . r 2 2 . R 2 − r 2 ≤ 4 R 6 27 2
Từ (1), (2) suy ra:
V = π 2 9 . 4 R 6 27 = 4 π 2 243 R 6 ⇒ V ≤ 2 π 9 3 R 3
Dấu “=” xảy ra khi:
⇔ r 2 2 = R 2 − r 2 ⇔ R 2 = 3 2 r 2 = 3 2 . k 2 R 2 4 π 2 ⇒ k 2 = 8 π 2 3 ⇒ k ≃ 5 , 13