Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

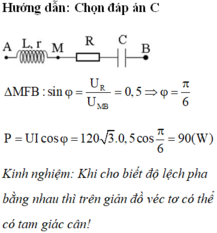
Chứng minh đk ,UrLvuông pha URC (vẽ giản đồ và kết hợp đk μAM=2μMB và ZL=ZC thì cm đk)
Suy ra U2=U2AM+UMB2 →Umb=120

Xét đoạn mạch MB có điện áp hiệu dụng gấp đôi điện áp hiệu dung trên R suy ra góc giữa \(U_{MB}\) và \(i\) là \(60^0\)
Mà \(u\) lệch pha \(90^0\) so với \(u_{MB}\)
Suy ra độ lệch pha giữa u và i là \(\varphi =30^0\)
Ta có:
\(P=U. I. \cos \varphi=120\sqrt 3.0,5.\cos30^0=90W\)

+ \(U_{AM}=I.Z_{AM}\), \(Z_{AM}\)không thay đổi, nên để \(U_{AM}\) đạt giá trị lớn nhất khi thay đổi C thì dòng điện Imax --> Xảy ra hiện tượng cộng hưởng: \(Z_L=Z_C\)
và \(I=\frac{U}{R+r}\)
Công suất của cuộn dây khi đó: \(P=I^2.r=\left(\frac{U}{R+r}\right)^2.r\) (*)
+ Nếu đặt vào 2 đầu AB một điện áp không đổi và nối tắt tụ C thì mạch chỉ gồm r nối tiếp với R (L không có tác dụng gì)
Cường độ dòng điện của mạch: \(I=\frac{25}{R+r}=0,5\Rightarrow R+r=50\)
Mà R = 40 suy ra r = 10.
Thay vào (*) ta đc \(P=\left(\frac{200}{50}\right)^2.10=160W\)
Bạn học đến điện xoay chiều rồi à. Học nhanh vậy, mình vẫn đang ở dao động cơ :(

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

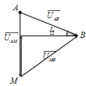
Biểu diễn vecto các điện áp. Vì U A M = U M B → AMB là tam giác cân tại M.
Từ giản đồ, ta có A ^ = B ^ = 90 0 − 15 0 = 75 0
→ φ M B = 75 0 − 15 0 = 60 0 → cos φ M B = 1 2
Đáp án C

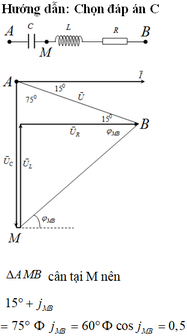
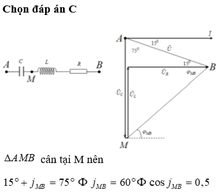
Biễu diễn vecto các điện áp. Mạch xảy ra cộng hưởng → U → cùng phương, chiều với vecto I → . Từ hình vẽ ta có:
U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ
Mặc khác, áp dụng định lý sin trong tam giác AMB:
U sin 180 − 3 φ = U A M sin φ → sin 3 φ − 5 4 sin φ = 0
→ 4 sin 3 φ − 7 4 sin φ = 0
Phương trình cho ta nghiệm sin φ = 7 4 → φ ≈ 41 0 .
→ U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ ≈ 240 V
Đáp án D