Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bảo toàn năng lượng toàn phần của mạch LC ta có: \(W=\frac{1}{2}Cu^2+\frac{1}{2}Li^2=\frac{1}{2}CU_0^2\)
\(\Rightarrow Li^2=C\left(U_0^2-u^2\right)\)
\(\Rightarrow i=\sqrt{\frac{C}{L}\left(U_0^2-u^2\right)}\)
Thay số ta được i = 6mA.
Đáp án C.

\(W= W_{Cmax}=W_C+W_L\)
=> \(W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)= 5.10^{-7}J.\)

\(C = \frac{1}{\omega^2.L}= 5.10^{-6}F.\)
\(U_0 = \frac{q_0}{C}= \frac{I_0}{C.\omega}= \frac{I_0.\sqrt{L}}{\sqrt{C}} = 8V.\)
\(i = I = \frac{I_0}{\sqrt{2}}. \)
\(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{u}{U_0}\right)^2 = 1- \left(\frac{i}{I_0}\right)^2 = 1 - \frac{1}{2}= \frac{1}{2}\)
=> \(u = \frac{1}{\sqrt{2}}U_0= 4\sqrt{2}V.\)

Ta có: \(\frac{1}{2}CU^2_{max}=\frac{1}{2}Li^2+\frac{1}{2}C^2_u\Rightarrow i=\sqrt{\frac{C}{L}\left(U^2_{max}-u^2\right)}\)\(=0,0447A=44,7mA\)
chọn D
\(\frac{1}{2}Li^2+\frac{1}{2}Cu^2=\frac{1}{2}CU_0^2\Rightarrow i=44,7mA\)
=> D đúng

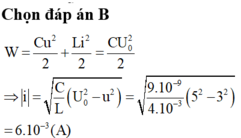



D