Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có : \(S=x_1+x_2=\dfrac{7}{2};P=x_1x_2=1\)
b) ta có \(S=x_1+x_2=\dfrac{-9}{2};P=x_1x_2=\dfrac{7}{2}\)
c) ta có : \(S=x_1+x_2=\dfrac{-4}{2-\sqrt{3}};P=x_1x_2=\dfrac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) ta có : \(S=x_1+x_2=\dfrac{3}{1,4}=\dfrac{15}{7};P=x_1x_2=\dfrac{1,2}{1,4}=\dfrac{6}{7}\)
e) ta có : \(S=x_1+x_2=\dfrac{-1}{5};P=x_1x_2=\dfrac{2}{5}\)
a) Theo hệ thức Vi-ét :
x1+x2=\(\frac{-b}{a}=\frac{7}{2}\)
x1x2=\(\frac{c}{a}=\frac{2}{2}=1\)
b) theo hệ thức Vi-ét:
x1+x2=\(\frac{-b}{a}=\frac{-9}{2}\)
x1x2=\(\frac{c}{a}=\frac{7}{2}\)
c)x1+x2=\(\frac{-b}{a}=\frac{-4}{2-\sqrt{3}}=-8-4\sqrt{3}\)
x1x2=\(\frac{c}{a}=\frac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) x1+x2=\(\frac{-b}{a}=\frac{3}{1,4}=\frac{15}{7}\)
x1x2=\(\frac{c}{a}=\frac{1,2}{1,4}=\frac{6}{7}\)
e) x1+x2=\(\frac{-b}{a}=\frac{-1}{5}\)
x1x2=\(\frac{c}{a}=\frac{2}{5}\)

Ta có: ∆ = - 7 2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 =-b/a =7/2 ; x 1 x 2 =c/a =2/2 =1

2 x 2 + 9x + 7 = 0
∆ = 9 2 - 4.2.7 = 81 - 56 = 25 > 0
Do đó, phương trình có hai nghiệm phân biệt
Theo hệ thức Vi – et ta có:
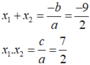

a) Ta có:Δ =(-7)2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =7/2 ;x1x2 =c/a =2/2 =1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5 ;x1x2 =c/a =-16/5
c) Ta có: Δ’ = 22 – (2 -√3 )(2 + √2 ) =4 -4 - 2√2 +2√3 +√6
= 2√3 - 2√2 +√6 >0
Phương trình 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
d) Ta có : Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/(1.4) = 30/14 = 15/7 ; x1x2 = c/a = (1.2)/(1.4) = 12/14 = 6/7
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0

Ta có : ∆ = - 3 2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x 1 + x 2 = -b/a = 3/(1,4) = 30/14 = 15/7 ; x 1 x 2 = c/a = (1,2)/(1,4) = 12/14 = 6/7
Ta có: Δ = 1 2 -4.5.2 = 1 - 40 = -39 < 0

(x2−2x+1+2)(2x−x2−1+7)=18(x2-2x+1+2)(2x-x2-1+7)=18
⇒[(x−1)2+2][7−(x−1)2]=18(1)⇒[(x-1)2+2][7-(x-1)2]=18(1)
Đặt (x−1)2=a(x-1)2=a
(1)⇔(a+2)(7−a)=18(1)⇔(a+2)(7-a)=18
⇒−a2+5a+14=18⇒-a2+5a+14=18
⇒a2−5a+4=0⇒a2-5a+4=0
Ta có a+b+c=1−5+4=0a+b+c=1-5+4=0
⇒a1=1⇒a1=1
a2=41=4a2=41=4
Thay (x−1)2=a(x-1)2=a vào ta được
[(x−1)2=1(x−1)2=4[(x−1)2=1(x−1)2=4
⇒⎡⎢ ⎢ ⎢⎣x−1=1x−1=−1x−1=2x−1=−2⇒[x−1=1x−1=−1x−1=2x−1=−2
⇒⎡⎢ ⎢ ⎢⎣x=2x=0x=3x=−1⇒[x=2x=0x=3x=−1
Vậy nghiệm của phương trình là x={−1;0;2;3}

Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: 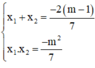
Khi đó:
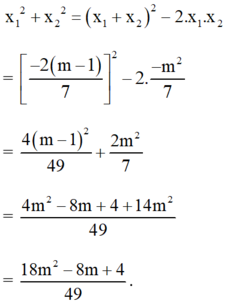

Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
\(x^2_1+x^2_2=\left(x_1+x_2\right)^2-2x_1x_2\\ =\left[\dfrac{-2\left(m-1\right)^2}{7}\right]-2\dfrac{\left(-m\right)^2}{7}\\ =\dfrac{4m^2-8m+4}{49}+\dfrac{2m^2}{7}\\ =\dfrac{4m^2-8m+4+14m^2}{49}\\ =\dfrac{18m^2-8m+4}{49}\)
Vậy \(x^2_1+x^2_2=\dfrac{18m^2-8m+4}{49}\).
Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
x\(\dfrac{1}{2}\)+x\(\dfrac{2}{2}\)=(x1+x2)2−2x1x2
=[\(\dfrac{-2\left(m-1\right)^2}{7}\)]-2\(\dfrac{\left(-m\right)^2}{7}\)
=\(\dfrac{4m^2-8m+4}{49}\)+\(\dfrac{2m^2}{7}\)
=\(\dfrac{4m^2-8m+4+14m^2}{49}\)
=\(\dfrac{18m^2-8m+4}{49}\)
vậy x\(\dfrac{2}{1}\)+x\(\dfrac{2}{2}\)=\(\dfrac{18m^2-8m+4}{49}\)
![]()
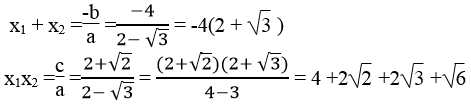
Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có: