Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: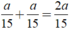
Ta có phương trình: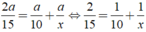
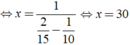
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.
Chọn đáp án C.

Hướng dẫn:
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: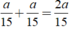
Ta có phương trình: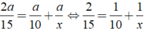
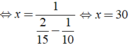
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.

Gọi x (phút ) là thời gian người khách dó đi từ A đến B
suy ra :Trong x phút người đo gắp x/15 chuyến xe buýt đi từ A đến Bđồng thời gắp x/10 chuyến xe buýt đi từ B tới A
Nếu khi đến B, người đó quay về A ngay thì trong x phút ,người đó gắp x/15 chuyến đi từ B về A đồng thời x/10 phút đi từ A về B
suy ra trong vòng 2x (phút) người đó gặp :x/15+x/10=x/5 (chuyến ) xe buýt đi từ A về B
Thời gian cấc xe lần lượt rời bến là : 2x:x/6=12 phút

Gọi x (phút ) là thời gian người khách đó đi từ A đến B
=> Trong x phút, người đó gặp \(\frac{x}{15}\) chuyến xe buýt đi từ A tới B đồng thời gặp \(\frac{x}{10}\) chuyến xe buýt đi từ B tới A
Nếu khi đến B, người đó quay về A ngay thì trong x phút: người đó gặp \(\frac{x}{15}\) chuyến đi từ B về A đồng thời \(\frac{x}{10}\) phút đi từ A về B
=> Trong vòng 2x (phút) người đó gặp : \(\frac{x}{15}\) + \(\frac{x}{10}\) = \(\frac{x}{6}\) (chuyến ) xe buýt đi từ A về B
=> Thời gian các xe lần lượt rời bến là sau: 2x : \(\frac{x}{6}\) = 12 phút
Gọi quãng đường nằm ngang là x
=> Thời gian đi trên đoạn nằm ngang đi về là 2x/15
=> Thời gian xuống dốc là 2(30 -x)/20 (xuống dốc lúc đi DB, xuống dốc lúc về AC, công lại chính là tổng đoạn đường trừ đi đường ngang)
=> Thời gian lên dốc là 2(30 -x)/10
*̀ 4h25 =4 + 5/12 = 53/12
Ta có phương trình
2[x/15 + (30 -x)/20 + (30-x)/10] = 53/12
Giải ra x

Gọi thời gian phải tìm là x (phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: \(\frac{a}{10}\)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: \(\frac{a}{x}\)
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: \(\frac{a}{15}+\frac{a}{15}=\frac{2a}{15}\)
Ta có phương trình: \(\frac{2a}{15}=\frac{a}{10}+\frac{a}{x}\Leftrightarrow\frac{2}{15}=\frac{1}{10}+\frac{1}{x}\Leftrightarrow x=\frac{1}{\frac{2}{15}-\frac{1}{10}}\Leftrightarrow x=30\)
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm

Giải:
Vẽ sơ đồ chuyển động mang tính khoa học
Gọi v1, s1, t1 là vận tốc, quãng đường và thời gian của xe 1.
Gọi v2, s2, t2 là vận tốc, quãng đường và thời gian của xe 2.
Đổi:
6 phút = 0,1h;
12 phút = 0,2h.
Khi 2 xe đi ngược chiều.
Quãng đường mà xe 1 đi được là:
ADCT:
thay số ta có ) (1a)
Quãng đường mà xe 2 đi được là:
ADCT:
thay số ta có )(2a)
Theo đề bài ta có s1 + s2 =6 (3a)
Từ (1a) , (2a) và (3a) ta lại có:
0,1v1 + 0.1v2 = 6 ( v1 + v2 =60. (4a)
Khi 2 xe đi cùng chiều.
Quãng đường mà xe 1 đi được là:
ADCT:
thay số ta có (1b)
Quãng đường mà xe 2 đi được là:
ADCT:
thay số ta có )(2b)
Theo đề bài ta có (3b)
Từ (1) , (2) và (3) ta lại có: (. (4b)
Giả sử xe thứ nhất có vận tốc lớn hơn xe thứ 2.
Kết hợp (4a) và (4b) ta có hệ phương trình (I)
Giải I ta có v1 = 35km/h và v2 = 25km/h
Giả sử xe thứ nhất có vận tốc nhỏ hơn xe thứ 2.
Kết hợp (4a )và (4b) ta có hệ phương trình (II)
Giải (II) ta có v1 = 25km/h và v2 = 35km/h
Đáp án D
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: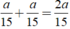
Ta có phương trình: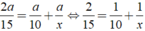
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.