Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

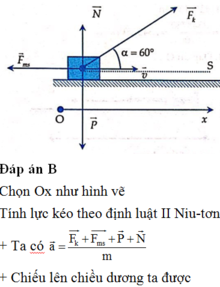
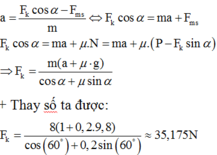
Tính quãng đường đi dựa vào công thức chuyển động thẳng biến đổi đều:
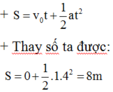
Công của lực kéo trong thời gian 5 giây kể từ khi bắt đầu chuyển động là
![]()

a) Công lực F
\(A_F=F.s=50.5=250\left(J\right)\)
b) Độ lớn lực ma sát:
\(F_{ms}=m.g.\mu=50.10.0,2=100\left(N\right)\)
Công lực ma sát:
\(A_{F_{ms}}=F_{ms}.s=100.5=500\left(J\right)\)
giải
a) công của lực F
\(A=F.S.\cos\left(0^o\right)=50.5.1=250\left(J\right)\)
b)công của lực ma sát
\(Fms=N.M=m.g.\mu=50.10.0,2=100\left(N\right)\)
công của lực ma sát là
\(Ams=Fms.S.\cos180^o=100.5.\left(-1\right)=-500\left(J\right)\)

a) (2 điểm)
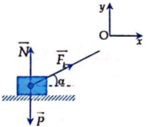
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật: (0,5 điểm)
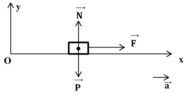
+ Viết phương trình định luật II Niu-tơn: 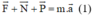 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (1) lên trục Ox ta được: F = m.a (0,5 điểm)
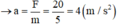 (0,5 điểm)
(0,5 điểm)
b) (2 điểm)
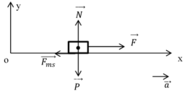
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật
+ Viết phương trình định luật II Niu-tơn
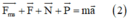 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (2) lên trục Oy: N – P = 0
→ N = P = m.g = 5.10 = 50N (0,5 điểm)
+ Độ lớn lực ma sát: F m s = μ.N = 0,2.50 = 10N (0,5 điểm)
+ Chiếu pt (2) lên trục Ox: F – F m s = ma
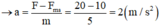 (0,5 điểm)
(0,5 điểm)

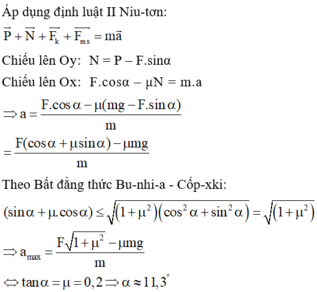
Chọn đáp án D