Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Electron chuyển động đều tức là lực điện cân bằng với lực từ:
\(F_E=F_B\)
\(\Rightarrow eE=evB\)
\(\Rightarrow v=\frac{E}{B}=10^6\left(\text{m/s}\right)\)
Động năng của electron:
\(T=\frac{m_ev^2}{2}\)
Năng lượng của photon cung cấp công thoát cho electron và cho electron vận tốc đầu (động năng):
\(h\frac{c}{\lambda}\text{=}E_{th}+T\) (\(E_{th}\)là công thoát)
\(\lambda=\frac{hc}{E_{th}+T}=1,7.10^{-7}\left(m\right)=0,17\left(nm\right)\)
\(chọn.A\)

Số lượng photon đến bản A bằng năng lượng của chùm photon chia cho năng lượng mỗi photon
\(N=\frac{Pt}{\varepsilon}\)
Số lượng electron bật ra là
\(N'=N.H=0,01N\)
Số electron đến bản B là
\(N''=\frac{q}{e}=\frac{It}{e}\)
Tỉ lệ số photon rời A đến được B là
\(\frac{N''}{N'}=\frac{I\varepsilon}{eHP}\approx0,218\)
Phần trăm rời A mà không đến B là
\(\text{1-0.218=0.782=78.2%}\)

Câu trả lời ở đây bạn nhé
Câu hỏi của lý - Học và thi online với HOC24

Động năng ban đầu cực đại của quang electron bứt ra từ mặt quả cầu:
\(\frac{mv^2_{max}}{2}=\frac{hc}{\lambda}-A=2,7.10^{-19}J\)
Gọi Q là điện tích của quả cầu, điện tích này phải là điện tích dương để giữ electron; điện tích Q phân bố đều trên mặt quả cầu, do đó điện thế trên mặt quả cầu là:
\(V=9.10^9.\frac{Q}{R}\). Trên quả cầu hình thành điện trường với các đường sức vuông góc với mặt cầu và hướng ra ngoài ( vì Q>0), điện trường này ngăn cản electron thoát ra khỏi quả cầu, công của điện trường cản là: \(W=eV=9.10^9.\frac{Qe}{R}\)
Muốn cho electron không thoát ra , công đó phải bằng động năng ban đầu cực đại của electron nghĩa là: \(9.10^9.\frac{Qe}{R}=\frac{mv^2_{max}}{2}\)
Thay số ta rút ra : \(Q=1,9.10^{-11}C\)

Giới hạn quang điện \(\lambda_0=\frac{hc}{A}=0,6\mu m\)
Trong ánh sáng trắng có các bước sóng \(\lambda\le\lambda_0\) nên có hiện tượng quang điện xảy ra .
+ \(v_{0max}\) ứng với \(\lambda_{min}=0,4\mu m\):
Từ \(\frac{hc}{\lambda_{min}}=A+\frac{1}{2}mv^2_{0max}\Rightarrow v_{0max}=\)\(\sqrt{\frac{2\left(\frac{hc}{\lambda_{min}}-A\right)}{m}}\)
\(\Leftrightarrow v_{0max}=\sqrt{\frac{\frac{2\left(6,625.10^{-34}.3.10^8\right)}{0,4.10^{-6}}-3,31.10^{-19}}{9,1.10^{-31}}}=\)\(0,6.10^6\left(m\text{/}s\right)\)

câu hỏi của bn có ở đây nhá Câu hỏi của HOC24 - Học và thi online với HOC24
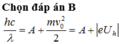
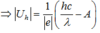
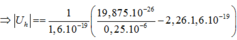
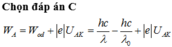
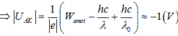
Chọn B