Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
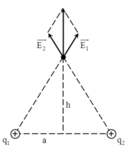
Cường độ điện trường tại điểm M là
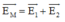
Trong đó E 1 → , E 2 → là cường độ điện trường do q 1 và q 2 gây ra tại M:
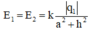
Suy ra: Cường độ điện trường tổng hợp tại M:
E M = 2 E 1 cos α = 2 k q h a 2 + h 2 1,5 V / m
Áp dụng bất đẳng thức Cô-si, ta có:
a 2 + h 2 = a 2 2 + a 2 2 + h 2 ≥ 3 a 4 h 2 4 3 ⇒ a 2 + h 2 3 ≥ 27 4 a 4 h 2
⇒ a 2 + h 2 3 2 ≥ 3 3 2 a 2 h
Vậy E M ≤ 2 k q h 3 3 2 a 2 h = 4 k q 3 3 a 2
EM cực đại khi h = a 2 ⇒ E M max = 4 k q 3 3 a 2

A B M C D N h P a a
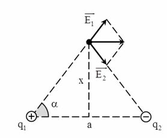
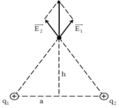
a) Vector cường độ điện trường tại M có phương và chiều được xác định như hình vẽ
Ta có \(|\overrightarrow{E_A}|=|\overrightarrow{MC}|=\frac{kq}{MA^2}=\frac{kq}{a^2+h^2}\)
\(\frac{MC}{MA}=\frac{MN}{2MP}\Rightarrow MN=\left|\overrightarrow{E_{AB}}\right|=\frac{2MC.MP}{MA}=\frac{2kqh}{\left(a^2+h^2\right)\sqrt{a^2+h^2}}\left(\frac{V}{m}\right)\)
b) Áp dụng BĐT Cauchy ta có:
\(E_{AB}=\frac{2kqh}{\sqrt{\left(a^2+h^2\right)^3}}=\frac{2kqh}{\sqrt{\left(\frac{a^2}{2}+\frac{a^2}{2}+h^2\right)^3}}\)
\(\le\frac{2kqh}{\sqrt{\left(3\sqrt[3]{\frac{a^4h^2}{4}}\right)^3}}=\frac{4kq}{3\sqrt{3}a^2}\)(không đổi)
Đạt được khi \(h=\frac{a\sqrt{2}}{2}.\)
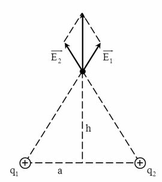
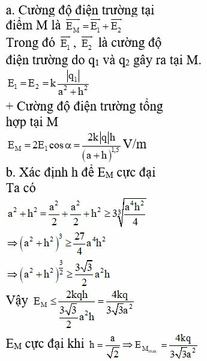


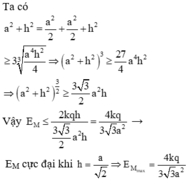
Đáp án C