Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGFAGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG

- Có 5 cách chọn chữ số hàng trăm.
- Có 5 cách chọn chữ số hàng chục.
- Có 4 cách chọn chữ số hàng đơn vị.
Số số được tạo thành là:
\(5.5.4=100\) (số)
Tuy nhiên trong 100 số này đã bị mất đi 1 số số chẵn:
| 012 | 013 | 014 | 015 |
| 021 | 023 | 024 | 025 |
| 031 | 032 | 034 | 035 |
| 041 | 042 | 043 | 045 |
| 051 | 052 | 053 | 054 |
Vậy số số lẻ hơn số số chẵn là 8 số.
Có số số chẵn là:
\(\left(100-8\right):2=46\) (số)
Có số số lẻ là :
\(100-46=54\) (số)
Nếu coi 100 số là 100 %.
Xác xuất chọn được số chẵn ở lần chọn đầu là:
\(46:100.100=46\%\)
Xác xuất chọn được số chẵn ở lần chọn thứ 2 (nếu lần ko trúng) là:
\(46:99.100\approx46,5\)

- Số các số tự nhiên có 5 chữ số khác nhau lập từ X=0;1;2;3;4;5X=0;1;2;3;4;5 là:
5.5!5.5!=600 (số)
- Tập hợp con gồm 5 phần tử của X mà tổng các chữ số chia hết cho 3 là:
{0,1,2,4,5}, {1,2,3,4,5}
Vậy số các số chia hết cho 3 có 5 chữ số khác nhau tạo bởi các số của X=0;1;2;3;4;5X=0;1;2;3;4;5 là: 4.4!+5!=216 (số). Nên còn lại 600-216=384 (số) không chia hết cho 3.
- Ta có tập hợp M có 600 (số ) nếu lấy hai số thì có C2600(cách).C6002(cách).
- Số cách lấy mà cả hai số đều không chia hết cho 3 là : C2384C3842, nên xác suất để lấy được cả hai số không chia hết cho 3 là : p1=C2384C2600p1=C3842C6002.
- Tóm lại xác suất để chọn hai số từ tập M mà hai số có ít nhất một số chia hết cho 3 là : p=1−p1=1−C2384C2600

1. số tự nhiên có dạng abce ( nhớ gạch trê đầu ( vì đây là số tự nhiên))
* ta có h là :
h= mn
trong đó tập hợp mn là {0,1}
=> có 2 trường hợp xảy ra
(m,n)=(1,0) hoặc (0,1)
* ta có số tự nhiên abhe có tập hợp {h,2,3,4,5,6,7,8,9}
a có 9 cách chọn
b có 8 cách chọn
c có 7 cách chọn
e có 6 cách chọn
vậy có 9*8*7*6=3024 số
*ta phải loại trường hợp h đứng đầu và có dạng 01
trường hợp h đứng đầu và có dạng 01 có số cách chọn là :
a có 1 cách chọn là h
b có 8 cách
c có 7 cách
e có 6 cách
=> có 1*8*7*6=336 số
vậy số tự nhiên theo yêu cầu đề bài có tổng cộng
3024 - 332688 số
0 chắc

Không gian mẫu: \(n_{\Omega}=A_8^5-A_7^4=5880\)
Chọn 3 chữ số chẵn: \(C_4^3=4\) cách
Chọn 2 chữ số lẻ: \(C_4^2=6\) cách
Xếp 2 số lẻ liền nhau, sau đó hoán vị với 3 chữ số chẵn: \(2!.4!=48\) cách
Chọn 3 chữ số chẵn sao cho có mặt chữ số 0: \(C_3^2=3\) cách
Hoán vị 5 chữ số sao cho 2 số lẻ liền nhau và số 0 đứng đầu: \(2!.3!=12\) cách
\(\Rightarrow6.\left(4.48-3.12\right)=936\)
Xác suất: \(P=\dfrac{936}{5880}=\dfrac{39}{245}\)

Chọn D
*) Ta có: ![]()
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có ![]() (cách).
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có ![]() cách.
cách.
Xếp hai chữ số 2 đứng liền nhau: Có ![]() cách.
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: ![]() (cách)
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: ![]() (cách)
(cách)
Vậy ![]()
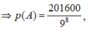

Chọn D
Gọi số có 6 chữ số có dạng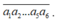
Từ 10 chữ số {0;1;2;3;4;5;6;7;8;9}, ta lập được 9. A 9 5 số có 6 chữ số đôi một khác nhau.
Lấy ngẫu nhiên một số từ tập X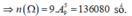
Gọi A là biến cố “Lấy một số thuộc X luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ ”.
Ta coi 3 vị trí liền nhau trong X là một phần tử Z, sắp xếp 3 chữ số khác nhau trong Z thỏa mãn biến cố :
+ Số thứ nhất là số lẻ thuộc Y có 3 cách chọn.
+ Số thứ hai là số chẵn thuộc Y có 2 cách chọn.
+ Số thứ ba là số lẻ thuộc Y có 2 cách chọn.
Áp dụng quy tắc nhân ta có 12 cách sắp xếp phần tử .
Trường hợp 1: Số có 6 chữ số có dạng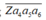
+) z có 12 cách chọn.
+) Xếp 5 chữ số còn lại khác các số tập Y vào 3 vị trí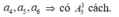
Áp dụng quy tắc nhân, ta lập được
Trường hợp2: Số có 6 chữ số có dạng
+) a 1 có 4 cách chọn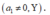
+) Xếp z vào 3 vị trí, z có 12 cách chọn nên có 36 cách sắp xếp.
+) Xếp 4chữ số còn lại vào 2 vị trí
Áp dụng quy tắc nhân, ta lập được 4.36. A 4 2 = 1728 số có 6 chữ số đôi một khác nhau thỏa mãn.
Vậy ta có tất cả (số) thoả mãn yêu cầu bài toán.
(số) thoả mãn yêu cầu bài toán.