K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
8 tháng 4 2016
\(5^x+5^{1-x}-6=0\)
<=> \(5^x+\frac{5}{5^x}-6=0\)
<=> \((5^x)^2-6.5^x+5=0\)
<=> \(5^x=5 \) hoặc \(5^x=1\)
<=> \(x=1 \) hoặc \(x=log_{5}{1}\)
Vậy phương trình đã cho có nghiệm: \(x=1 \) hoặc \(x=log_{5}{1}\)
8 tháng 4 2016
\(5^x+5^{1-x}-6=0\Leftrightarrow5^{2x}-6.5+5=0\)
\(\Leftrightarrow\begin{cases}5^x=5\\5^x=1\end{cases}\)
\(\Rightarrow\begin{cases}x=1\\x=0\end{cases}\)
Q
7 tháng 6 2017
a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)
2 tháng 4 2017
a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}
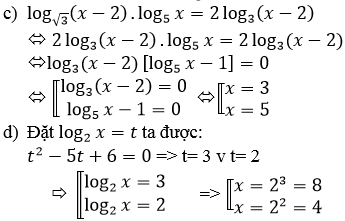
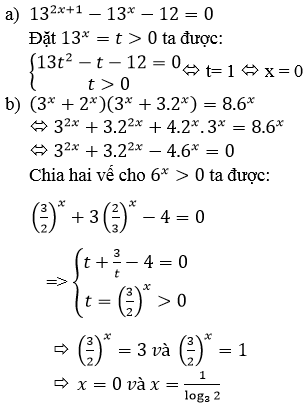
⇔ x = 1