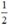Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
5x2−3x=0⇔x(5x−3)=05x2−3x=0⇔x(5x−3)=0
⇔ x = 0 hoặc 5x – 3 =0
⇔ x = 0 hoặc x=35.x=35. Vậy phương trình có hai nghiệm: x1=0;x2=35x1=0;x2=35
Δ=(−3)2−4.5.0=9>0√Δ=√9=3x1=3+32.5=610=35x2=3−32.5=010=0Δ=(−3)2−4.5.0=9>0Δ=9=3x1=3+32.5=610=35x2=3−32.5=010=0
b)
3√5x2+6x=0⇔3x(√5x+2)=035x2+6x=0⇔3x(5x+2)=0
⇔ x = 0 hoặc √5x+2=05x+2=0
⇔ x = 0 hoặc x=−2√55x=−255
Vậy phương trình có hai nghiệm: x1=0;x2=−2√55x1=0;x2=−255
Δ=62−4.3√5.0=36>0√Δ=√36=6x1=−6+62.3√5=06√5=0x2=−6−62.3√5=−126√5=−2√55Δ=62−4.35.0=36>0Δ=36=6x1=−6+62.35=065=0x2=−6−62.35=−1265=−255
c)
2x2+7x=0⇔x(2x+7)=02x2+7x=0⇔x(2x+7)=0
⇔ x = 0 hoặc 2x + 7 = 0
⇔ x = 0 hoặc x=−72x=−72
Vậy phương trình có hai nghiệm: x1=0;x2=−72x1=0;x2=−72
Δ=72−4.2.0=49>0√Δ=√49=7x1=−7+72.2=04=0x2=−7−72.2=−144=−72Δ=72−4.2.0=49>0Δ=49=7x1=−7+72.2=04=0x2=−7−72.2=−144=−72
d)
2x2−√2x=0⇔x(2x−√2)=02x2−2x=0⇔x(2x−2)=0
⇔ x = 0 hoặc 2x−√2=02x−2=0
⇔ x = 0 hoặc x=√22x=22
Δ=(−√2)2−4.2.0=2>0√Δ=√2x1=√2+√22.2=2√24=√22x2=√2−√22.2=04=0

a, \(\Delta=25-8=17\)>0 Vậy pt có 2 nghiệm pb
\(x=\dfrac{5\pm\sqrt{17}}{4}\)
b, \(\Delta=16-16=0\)Vậy pt có nghiệm kép
\(x_1=x_2=\dfrac{1}{4}\)
c, \(\Delta=1-4.2.5< 0\)Vậy pt vô nghiệm
d, \(\Delta=4+4.24=100>0\)Vậy pt có 2 nghiệm pb
\(x=\dfrac{-2-10}{-6}=2;x=\dfrac{-2+10}{-6}=-\dfrac{4}{3}\)

a) ta có : \(S=x_1+x_2=\dfrac{7}{2};P=x_1x_2=1\)
b) ta có \(S=x_1+x_2=\dfrac{-9}{2};P=x_1x_2=\dfrac{7}{2}\)
c) ta có : \(S=x_1+x_2=\dfrac{-4}{2-\sqrt{3}};P=x_1x_2=\dfrac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) ta có : \(S=x_1+x_2=\dfrac{3}{1,4}=\dfrac{15}{7};P=x_1x_2=\dfrac{1,2}{1,4}=\dfrac{6}{7}\)
e) ta có : \(S=x_1+x_2=\dfrac{-1}{5};P=x_1x_2=\dfrac{2}{5}\)
a) Theo hệ thức Vi-ét :
x1+x2=\(\frac{-b}{a}=\frac{7}{2}\)
x1x2=\(\frac{c}{a}=\frac{2}{2}=1\)
b) theo hệ thức Vi-ét:
x1+x2=\(\frac{-b}{a}=\frac{-9}{2}\)
x1x2=\(\frac{c}{a}=\frac{7}{2}\)
c)x1+x2=\(\frac{-b}{a}=\frac{-4}{2-\sqrt{3}}=-8-4\sqrt{3}\)
x1x2=\(\frac{c}{a}=\frac{2+\sqrt{2}}{2-\sqrt{3}}\)
d) x1+x2=\(\frac{-b}{a}=\frac{3}{1,4}=\frac{15}{7}\)
x1x2=\(\frac{c}{a}=\frac{1,2}{1,4}=\frac{6}{7}\)
e) x1+x2=\(\frac{-b}{a}=\frac{-1}{5}\)
x1x2=\(\frac{c}{a}=\frac{2}{5}\)

Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
\(x^2_1+x^2_2=\left(x_1+x_2\right)^2-2x_1x_2\\ =\left[\dfrac{-2\left(m-1\right)^2}{7}\right]-2\dfrac{\left(-m\right)^2}{7}\\ =\dfrac{4m^2-8m+4}{49}+\dfrac{2m^2}{7}\\ =\dfrac{4m^2-8m+4+14m^2}{49}\\ =\dfrac{18m^2-8m+4}{49}\)
Vậy \(x^2_1+x^2_2=\dfrac{18m^2-8m+4}{49}\).
Xét phương trình 7x2 + 2(m – 1)x – m2 = 0 (1)
a) Phương trình có nghiệm khi ∆’ ≥ 0
Ta có: ∆’ = (m – 1)2 – 7(-m2) = (m – 1)2 + 7m2 ≥ 0 với mọi m
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của m
b) Gọi x1, x2 là hai nghiệm của phương trình (1)
Ta có:
x\(\dfrac{1}{2}\)+x\(\dfrac{2}{2}\)=(x1+x2)2−2x1x2
=[\(\dfrac{-2\left(m-1\right)^2}{7}\)]-2\(\dfrac{\left(-m\right)^2}{7}\)
=\(\dfrac{4m^2-8m+4}{49}\)+\(\dfrac{2m^2}{7}\)
=\(\dfrac{4m^2-8m+4+14m^2}{49}\)
=\(\dfrac{18m^2-8m+4}{49}\)
vậy x\(\dfrac{2}{1}\)+x\(\dfrac{2}{2}\)=\(\dfrac{18m^2-8m+4}{49}\)
![]()

a) Phương trình bậc hai
2 x 2 – 7 x + 3 = 0
Có: a = 2; b = -7; c = 3;
Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 2 . 3 = 25 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
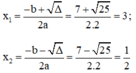
Vậy phương trình có hai nghiệm là 3 và 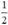
b) Phương trình bậc hai 6 x 2 + x + 5 = 0
Có a = 6; b = 1; c = 5;
Δ = b 2 – 4 a c = 12 – 4 . 5 . 6 = - 119 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 6 x 2 + x – 5 = 0
Có a = 6; b = 1; c = -5;
Δ = b 2 – 4 a c = 12 – 4 . 6 . ( - 5 ) = 121 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
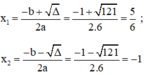
Vậy phương trình có hai nghiệm là -1 và 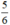
d) Phương trình bậc hai 3 x 2 + 5 x + 2 = 0
Có a = 3; b = 5; c = 2;
Δ = b 2 – 4 a c = 5 2 – 4 . 3 . 2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
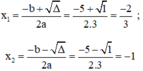
Vậy phương trình có hai nghiệm là -1 và 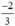
e) Phương trình bậc hai y 2 – 8 y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b 2 – 4 a c = ( - 8 ) 2 – 4 . 1 . 16 = 0 .
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
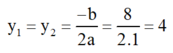
Vậy phương trình có nghiệm kép y = 4.
f) Phương trình bậc hai 16 z 2 + 24 z + 9 = 0
Có a = 16; b = 24; c = 9; Δ = b 2 – 4 a c = 24 2 – 4 . 16 . 9 = 0
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép:
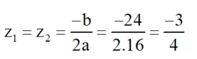
Vậy phương trình có nghiệm kép 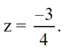
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 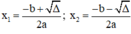
+ Nếu Δ = 0, phương trình có nghiệm kép 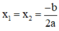 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
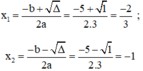
Vậy phương trình có hai nghiệm là -1 và 

Lời giải
a)\(\left\{{}\begin{matrix}a=7\\b=-2\\c=3\end{matrix}\right.\) \(\Rightarrow\Delta'=1-21=-20< 0\Rightarrow\left(a\right)VoN_0\)
(b) \(\left\{{}\begin{matrix}a=5\\b=2\sqrt{10}\\c=2\end{matrix}\right.\) \(\Rightarrow\Delta'=10-10=0\Rightarrow\left(b\right)\) có một nghiệm kép
(c) \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=7\\c=\dfrac{2}{3}\end{matrix}\right.\) \(\Rightarrow\Delta=49-4.\dfrac{1}{2}.\dfrac{2}{3}=49-\dfrac{4}{3}=\dfrac{143}{3}>0\) có hai nghiệm phân biệt
(d) \(\left\{{}\begin{matrix}a=1,7\\b=-1,2\\c=-2,1\end{matrix}\right.\) \(\Delta'=0,6^2+2,1.1,7>0\) pt có hai nghiệm phân biệt

Phương trình bậc hai 2x2 – 7x + 3 = 0
Có: a = 2; b = -7; c = 3; Δ = b2 – 4ac = (-7)2 – 4.2.3 = 25 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
Vậy phương trình có hai nghiệm là 3 và