Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
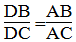
Suy ra:
Suy ra:
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
b. Ta có: SABC =1/2.AB.AC =1/2.AH.BC
Suy ra: AB.AC = AH.BC
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90o
Theo định lí Pi-ta-go, ta có: AB2 = AH2 + HB2
Suy ra: HB2 = AB2 - AH2 = 122 - (9,6)2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠(AHD) = 90o
Theo định lí Pi-ta-go, ta có:
AD2 = AH2 + HD2 = (9,6)2 + (1,37)2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)

Tự vẽ hình chỉ bt làm ý a,c, thôi thông cảm T^T
a,Xét ΔHAB và ΔABC
\(\widehat{BHA}=\widehat{BAH}=90^o\)
Góc B chung
\(\Rightarrow\Delta HBA\text{∼ }\Delta ABC\)
c,Xét ΔABC ta có:
BC2=AC2+AB2
BC2=162+122
BC2=400
BC=√400=20cm
Ta có ΔHAB~ΔABC(câu a)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12.16}{20}=9,6cm\)
a.Xét \(\Delta HBA\)và \(\Delta ABC\)có
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{B}\) chung
Do đó \(\Delta HBA\)đồng dạng \(\Delta ABC\)\((\)g.g\()\)
b.Từ \(\Delta HBA\)đồng dạng \(\Delta ABC\)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\)
\(\Rightarrow AH.BC=AB.AC\)
c.Xét \(\Delta ABC\),có \(\widehat{A}\)=90 độ , theo định lý py -ta -go,ta có
\(BC^2=AB^2+AC^2\)
\(BC^2=12^2+16^2\)
\(BC^2=400\)\(\Rightarrow BC=\sqrt{400}\)
\(BC=20cm\)
Ta có \(\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12\times16}{20}\)
\(\Rightarrow AH=9,6cm\)
Chúc bạn học tốt.Phần d mình chưa giải đc nha

Tk mình đi mọi người mình bị âm nè!
Ai tk mình mình tk lại cho!

A B C H D E F
a) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Xét tam giác ABC có AD là đường phân giác trong của tam giác ABC (gt)
\(\Rightarrow\frac{BD}{DC}=\frac{AB}{AC}\left(tc\right)\)
\(\Rightarrow\frac{BD}{DC}=\frac{3}{4}\)
\(\Rightarrow\frac{BD}{3}=\frac{DC}{4}=\frac{BD+DC}{3+4}\frac{10}{7}\)(tính chất của dãy tỉ số bằng nhau )
\(\Rightarrow\hept{\begin{cases}BD=\frac{10}{7}.3=\frac{30}{7}\left(cm\right)\\DC=\frac{10}{7}.4=\frac{40}{7}\left(cm\right)\end{cases}}\)
b)Ta có: \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC\)
\(\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)
c) Xét tam giác ADB có DE là đường phân giác trong của tam giác ADB(gt)
\(\Rightarrow\frac{EA}{EB}=\frac{AD}{BD}\left(tc\right)\)
Xét tam giác ADC có DF là đường phân giác trong của tam giác ADC (gt)
\(\Rightarrow\frac{FC}{FA}=\frac{DC}{DA}\left(tc\right)\)
\(\Rightarrow\frac{EA}{EB}.\frac{DB}{DC}.\frac{FC}{FA}=\frac{AD}{BD}.\frac{DB}{DC}.\frac{DC}{DA}=1\left(đpcm\right)\)

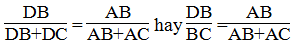
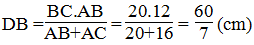
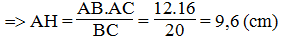
Lời giải:
a) Vì tam giác $ABC$ vuông tại $A$ nên:
$S_{ABC}=\frac{AB.AC}{2}$
Mặt khác: $S_{ABC}=\frac{AH.BC}{2}$
$\Rightarrow AB.AC=AH.BC$ (đpcm)
b) Áp dụng định lý Pitago cho tam giác $ABC$ vuông:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
Áp dụng định lý Pitago cho tam giác $ABH$ vuông:
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BD+DC}=\frac{BD}{BC}=\frac{3}{3+4}$
$\Rightarrow BD=BC.\frac{3}{7}=\frac{60}{7}$ (cm)
$DC=BC-BD=20-\frac{60}{7}=\frac{80}{7}$ (cm)
Hình vẽ: